2 sigma or standard deviation is used to understand variability when performing data analysis. It checks if the numbers are clustered together or spread out and identifies data points that are 2 standard deviations away from the mean. In this guide, we will go through step by step guide on how to calculate 2 sigma in Excel.
5 Key Takeaways
- 2 Sigma represents two standard deviations from the mean.
- It helps in identifying outliers and maintaining data consistency.
- Use the AVERAGE and STDEV.S to calculate the mean and standard deviation.
- In finance, it helps measure volatility and the risk of an investment.
- It plays an important role in quality control by checking if the product is within acceptable limits.
Table of Contents
2 Sigma in Excel
Explanation
2 sigma is a statistical term that is used to measure the variability or deviation of the data. It can help identify outliers in your data and provides consitentcy and reliability. For a normal distribution,
- 1 sigma represents values that are within 1 standard deviation of the mean. 68% of the data fall within this range.
- 2 sigma represents values that are within 2 standard deviations of the mean. 95% of the data fall within this range.
Standard Deviation in Data Analysis
Standard deviation shows how much your data varies from the average value. It tells us whether the data is cluttered or close together. It is a risk assessment tool for data analysts. In manufacturing, a low standard deviation means that the product has high qualitycontrol and is consistent. Whereas, in finance, a low standard deviation will mean that the investment has lower volatility.
Steps to Calculate 2 Sigma
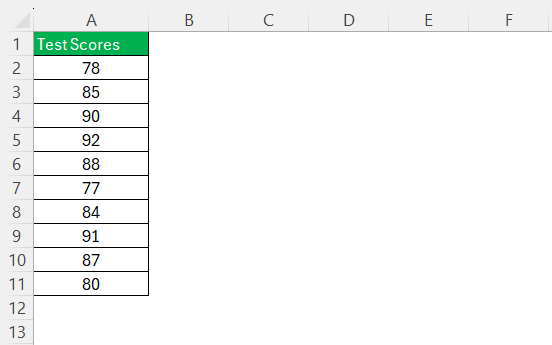
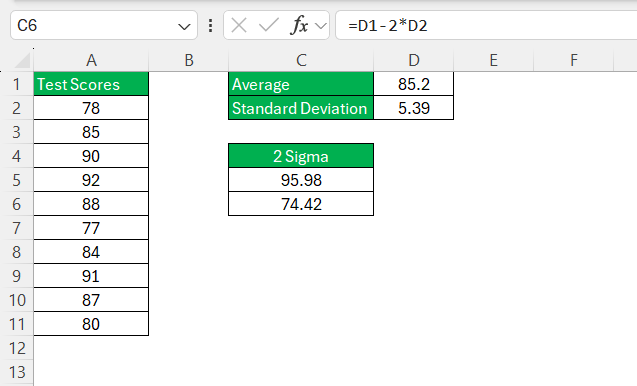
STEP 1: Enter the data into a column.
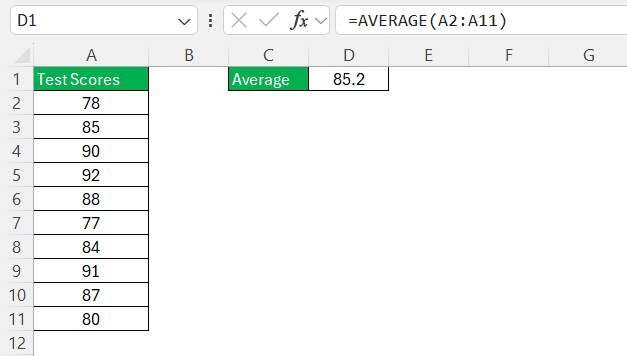
STEP 2:In an empty cell, type the formula
=AVERAGE(A2:A11)
This will calculate the average value.
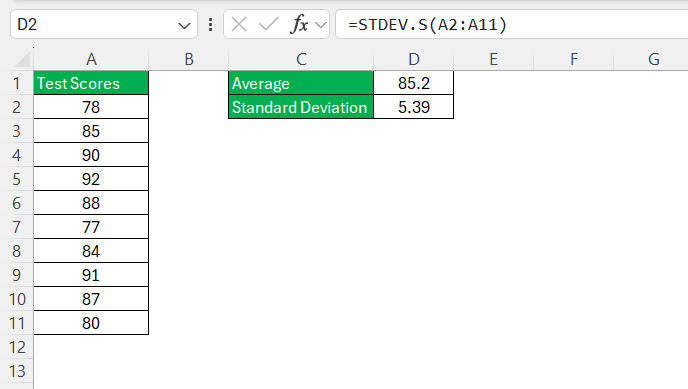
STEP 3: In another cell, use the standard deviation function
=STDEV.S(A2:A11)
This will calculate the standard deviation.
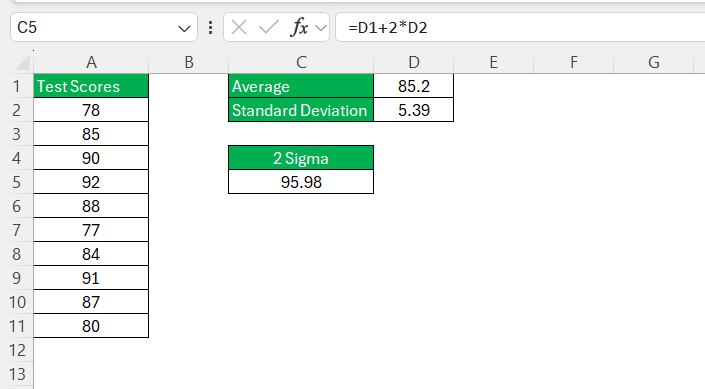
STEP 4: In a new cell, type
=D1 + 2 * D2
This will calculate the upper bound (Mean + 2 Sigma).
Next, type
=D1 – 2 * D2
This will calculate the lower bound (Mean – 2 Sigma).
Now, I have the 2 sigma range of 74.42 to 95.98. Data within this range is considered typical, while anything outside could be an outlier.
Common Pitfalls and How To Avoid Them
Before starting with the calculations of 2 sigma, it is important to make sure that the data is accurate. This is because if we input incorrect data, our results would also be incorrect. Also, check if the is data formatting is correct and consistent. Excel distinguishes between numbers and text, and will exclude text from any numerical formulas.
Reviewing datasets to spot extreme outliers is also an important and useful practice. Such deviations could either indicate an error in data or a unique event that should be separately categorized in the analysis.
Taking these cautionary steps before calculation will guarantee accurate results and build confidence in the quality of your analysis.
Real-World Applications of 2 Sigma
In Manufacturing
In the manufacturing sector, the application of 2 sigma is for quality control and for product consistency. By tracking the standard deviation of the dimensions of a manufactured product, you can check if the product is within the required tolerance level. A low sigma value indicates that the products are nearly identical and have very little variation. Whereas a high sigma value will indicate that the products vary more and would signal problems like worn-out tools or machines.
By applying 2 sigma in manufacturing, you can aim at the reduction of defective products, hence increasing customer satisfaction and reputation. This monitoring system helps in spotting any issue early and fixing it before it turns into bigger problem. This approach helps in consistent quality and keeps production running smoothly.
In Financial Markets
In financial markets, 2 sigma is used to calculate how much the investment returns vary. If the value is high, it means that the investment is more volatile and has more risk. Whereas a low sigma value means investment is steadier and more predictable.
Standard deviation helps investor is setting risk limits for their portfolio and check how to diversify it to reduce risk. It is a key tool to help investors make informed decisions.
FAQs
What is a 2 sigma calculation?
2 sigma is statiscal measure that is used to find 2 standard deviations from the mean of the dataset. It covers about 95% of data points under a normal distribution. It checks the variability and consistency of data, making it important for quality control.
What are the steps to get 2 standard deviations?
Start by calculating the mean of the values using the AVERAGE function. Next, use the STDEV function to calculate the standard deviation of the data. Lastly, multiply the standard deviation by 2 and add or subtract it from the mean value ot get 2 sigma.
What is the role of standard deviation in data analysis?
Standard deviation shows how much the data varies from the mean. It helps determine if the numbers are clustered together or spread out. This, in turn, helps in understanding and identifying consistency in the dataset.
What are some common mistakes when calculating 2 sigma in Excel?
The common mistakes that you can make when calculating 2 sigma are:
- Incorrect data entry
- Using the population standard deviation formula when working with sample data
- Not taking into account the outliers
It is important to make sure that the data is correct so the results of your analysis are accurate.
What are the real world uses of 2 sigma?
The real-world applications of 2 sigma are:
- To maintain product quality in manufacturing.
- To assess investment risk in finance.
- To support quality control.
- To identify outliers.
John Michaloudis is a former accountant and finance analyst at General Electric, a Microsoft MVP since 2020, an Amazon #1 bestselling author of 4 Microsoft Excel books and teacher of Microsoft Excel & Office over at his flagship MyExcelOnline Academy Online Course.
30 Days - Full Access 
