How to Use the ATAN2 Function in Excel

When working with angles and coordinates in Excel, I often find myself using the ATAN2 function. It’s an incredibly useful tool for calculating the arctangent of two numbers, which comes in handy when dealing with trigonometry, navigation, and geometry-related tasks.

In this article, I’ll walk you through everything you need to know about the ATAN2 function, including its syntax, usage, and real-world applications.

Key Takeaways:

• The ATAN2 function calculates the angle between two points relative to the origin, returning values in radians from -π to π.
• Unlike ATAN, ATAN2 considers both x and y coordinates, making it useful for determining angles in all four quadrants.
• ATAN2 is widely used in navigation, robotics, game development, and physics for precise directional calculations.
• To convert radians to degrees, use the DEGREES function, e.g., =DEGREES(ATAN2(y, x)).
• Common errors include non-numeric inputs (#VALUE!) and zero inputs (#DIV/0!), which should be handled carefully.

 

Getting Started with ATAN2

What is ATAN2 Function?

The ATAN2 function in Excel is a powerful tool for calculating the angle between two points, described by their coordinates, with respect to the origin (0,0). The ATAN2 function in Excel calculates the arctangent (inverse tangent) of the ratio of two specified numbers, typically representing the Y and X coordinates of a point.

Syntax of ATAN2: =ATAN2(y_num, x_num)

• y_num – The Y-coordinate (vertical value).
• x_num – The X-coordinate (horizontal value).

The function returns an angle in radians, ranging from -π to π (-180° to 180°).

Difference Between ATAN and ATAN2

The primary difference between the ATAN and ATAN2 functions lies in their handling of coordinate signs and quadrants. The ATAN function computes the arctangent of a single value, effectively limiting its output to the first and fourth quadrants. It does so by assuming a positive or negative x-axis.

In contrast, ATAN2 considers both x and y coordinates, allowing it to accurately determine the correct angle across all four quadrants. This feature makes ATAN2 more versatile, as it delivers a full-circle perspective, which is crucial for directional calculations where the quadrant is significant. Thus, while ATAN might suffice for simple calculations, ATAN2 offers a complete understanding needed for advanced navigation and data analysis tasks.

 

How to Use the ATAN2 Function

1. Basic Example

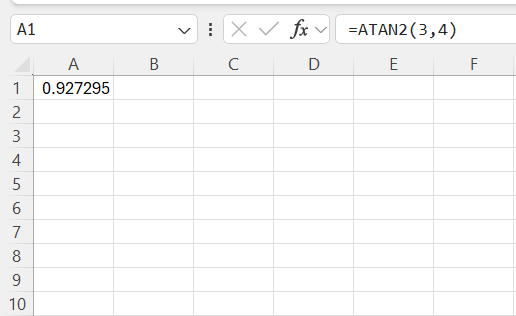
Let’s say I have a point (3, 4) on a Cartesian plane, and I want to calculate the angle it makes with the x-axis. I can use the following formula:

=ATAN2(3, 4)

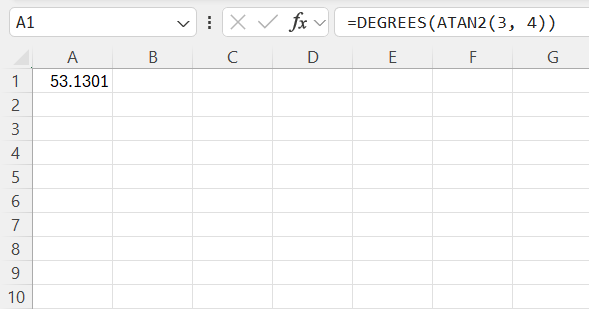
This returns 0.927 radians, which is approximately 53.13° when converted using the DEGREES function:

=DEGREES(ATAN2(3, 4))

The output is 53.13°.

2. Understanding Quadrants

One of the best features of ATAN2 is that it correctly identifies angles in all four quadrants:

• Quadrant I (X > 0, Y > 0) – Positive angle (0 to 90°)
• Quadrant II (X < 0, Y > 0) – Positive angle (90 to 180°)
• Quadrant III (X < 0, Y < 0) – Negative angle (-180 to -90°)
• Quadrant IV (X > 0, Y < 0) – Negative angle (-90 to 0°)

For example:

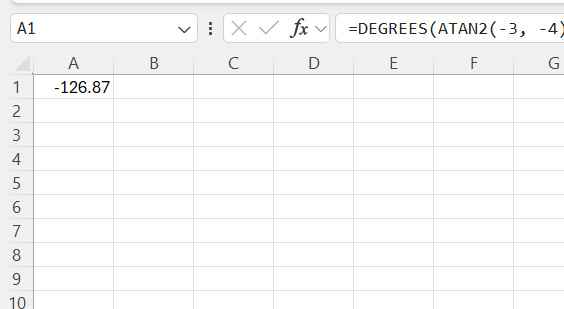
=DEGREES(ATAN2(-3, -4))

This returns -126.87°, placing the point in the third quadrant.

3. Using ATAN2 for Directional Calculations

In navigation and GIS (Geographic Information Systems), I often use ATAN2 to find the bearing angle between two points. If I have two coordinates (X1, Y1) and (X2, Y2), the direction from one to the other is given by:

=DEGREES(ATAN2(Y2 – Y1, X2 – X1))

This formula calculates the correct angle for movement from one point to another, which is crucial in mapping and route optimization.

4. Converting Radians to Degrees

Since Excel’s trigonometric functions return values in radians, I always use the DEGREES function when I need results in degrees:

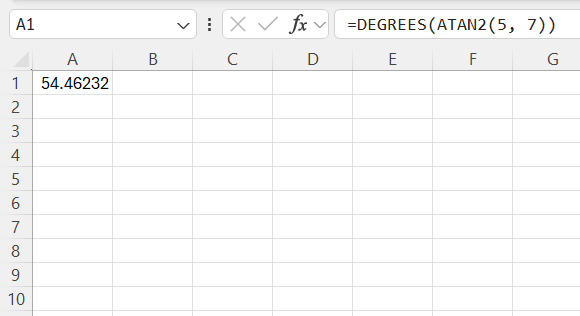
=DEGREES(ATAN2(5, 7))

This gives an output of approximately 54.46°.

 

Practical Applications of the ATAN2 Function

The ATAN2 function has various practical applications across different fields, allowing for precise angle calculations in scenarios involving two-dimensional coordinates.

1. Robotics and Motion Control

In robotics, I use ATAN2 to determine the direction a robot should move based on target coordinates. By calculating the angle between the robot’s current position and the target, I can adjust its orientation accordingly. This is particularly useful for autonomous robots navigating through obstacles or robotic arms aligning with objects.

It ensures smooth, precise movement and helps in path planning algorithms, such as SLAM (Simultaneous Localization and Mapping).

2. Game Development

Game developers often use ATAN2 to calculate the angle of rotation for characters or objects moving in a 2D space. For instance, if a player moves towards an enemy, the game can use ATAN2 to rotate the enemy in the correct direction. This is also useful in aiming mechanics, where projectiles must follow a realistic trajectory towards a target.

Additionally, ATAN2 assists in character movement for AI-controlled entities, ensuring fluid navigation and interaction with dynamic game elements.

3. Engineering and Physics

In engineering simulations and physics calculations, ATAN2 is useful for analyzing vectors, projectile motion, and mechanical systems that involve angular movement. It helps engineers determine torque, angular displacement, and force directions in dynamic systems.

In fluid dynamics, ATAN2 is used to compute flow directions and streamline patterns, which are crucial for designing efficient aerodynamic structures and hydraulic systems.

4. Financial and Business Applications

Some financial models incorporate ATAN2 to calculate trends and directional changes in stock market analysis or logistic optimization. In technical analysis, ATAN2 can be applied to vector-based indicators to measure momentum and trend shifts.

In supply chain management, it helps optimize delivery routes by determining the shortest path and angle between warehouses and distribution points, improving efficiency in logistics and transportation planning.

 

Common Errors and Troubleshooting

While using ATAN2, I sometimes encounter errors:

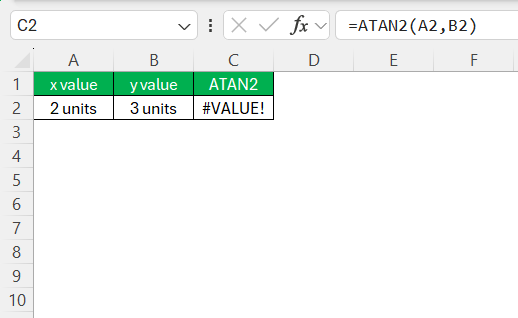
#VALUE! Error – This happens if non-numeric values are used as arguments.

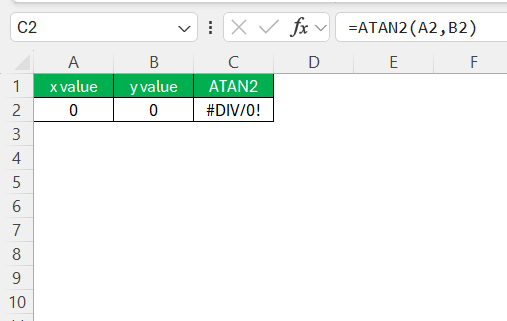
Zero Inputs – If both X and Y are zero (ATAN2(0,0)), Excel returns #DIV/0! because the function requires a valid ratio.

These rules ensure that even with negative coordinates, the ATAN2 function provides an accurate representation of angles, essential for comprehensive data analysis and practical applications across various fields.

 

FAQs

How to calculate atan in Excel?

To calculate ATAN in Excel, you can use the ATAN function. Simply enter =ATAN(number) into a cell, where “number” is the value for which you want to find the arctangent. The function returns the angle in radians between -π/2 and π/2. If you need the result in degrees, wrap it with the DEGREES function: =DEGREES(ATAN(number)).

What is the difference between ATAN and ATAN2 functions?

The ATAN function calculates the arctangent of a single number, providing an angle between -π/2 and π/2 in radians. It considers just one axis. In contrast, the ATAN2 function takes two arguments, allowing it to determine the angle relative to the positive x-axis, accounting for all four quadrants. ATAN2’s two-argument capability makes it more versatile for directional calculations.

How can I ensure accuracy when using ATAN2?

To ensure accuracy when using the ATAN2 function, double-check the order of the x and y coordinates (as ATAN2(y, x)), verify the input data’s precision, and convert the result from radians to degrees if needed. Use named ranges for better clarity, and compare calculated angles to expected values to confirm correctness.

Can ATAN2 be used with other Excel functions?

Yes, ATAN2 can be effectively combined with other Excel functions to enhance data analysis. It’s often used with mathematical functions like SUM and AVERAGE to summarize or average directional angles. Additionally, it can be paired with IF for conditional logic based on angle values, or wrapped in DEGREES for converting radians to degrees, improving interpretability.

Why use atan2?

Using ATAN2 is beneficial because it accurately calculates angles considering all four quadrants, making it ideal for directional and navigational applications. Unlike ATAN, which handles only positive angles, ATAN2 considers the signs of both x and y coordinates, ensuring correct angle determination relative to the positive x-axis.