How to Calculate Confidence Interval in Excel

• A confidence interval is a range of values within which the population parameter is likely to exist.
• Use the CONFIDENCE function to calculate this range of values.
• The confidence level tells you how reliable the estimate is.
• Common errors can be avoided by using correct syntax and valid inputs.
• It provides certainty in decision-making.

 

What is a Confidence Interval?

A confidence interval is a range of values within which the population parameter is likely to exist. It provides a range instead of a single value based on repeated sample data. Instead of telling you that the customer satisfaction score as per the survey is on average 8 out of 10. It tells you that the score will be between 7.6 and 8.4.

The confidence levels tell you how accurate your estimate is. For example, if the confidence level is 95%, it means that 95 out of 100 times the actual parameter will lie within the calculated range.

This measure is important because:

• It shows accuracy, not averages.
• It provides reliability and helps in decision-making.
• It allows fair comparison between datasets.
• It helps in predicting customer behaviour.

 

How to Calculate Confidence Intervals

Preparing Your Data

Before starting with the calculations, make sure that the data is properly organized in a table format. Each column should have a header for easy identification. Always double-check to avoid any gaps or anomalies that can skew your results.

Syntax for Confidence Interval

The CONFIDENCE function is used to calculate the confidence interval for the data. The syntax for this function is:

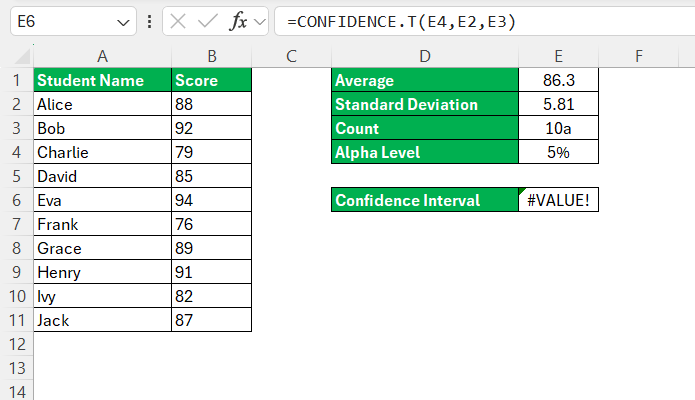
=CONFIDENCE(alpha, standard_dev, size)

• alpha: The significance level, which is equal to 1 minus the confidence level. For example, for a 95% confidence level, the alpha would be 0.05 (since 1 – 0.95 = 0.05).
• standard_dev: The standard deviation of your data set. This should be the population standard deviation if known; otherwise, you might estimate it using the sample standard deviation.
• size: The size of the sample, which is the number of observations in your data set.

This function will return the margin of error, which you can add and subtract from the mean to get the confidence interval.

Steps to Calculate Confidence Interval

Follow the steps below to calculate a confidence interval in Excel –

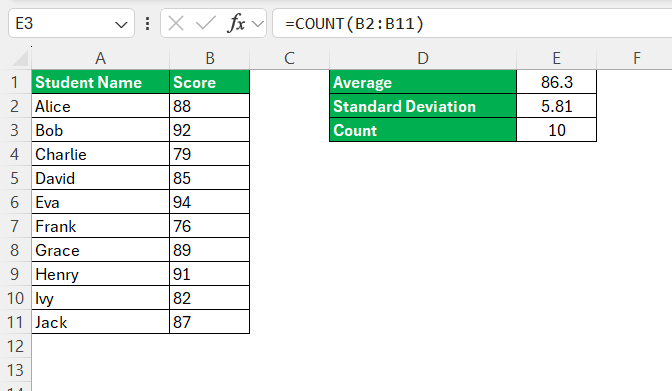
STEP 1: Make sure that your data is organized in a single column in Excel.

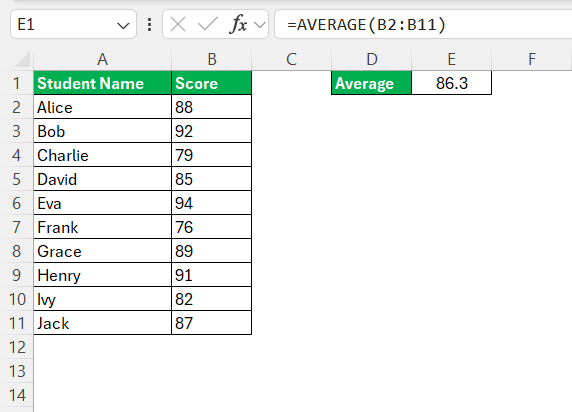
STEP 2: In an empty cell, use the AVERAGE function to calculate the sample mean.

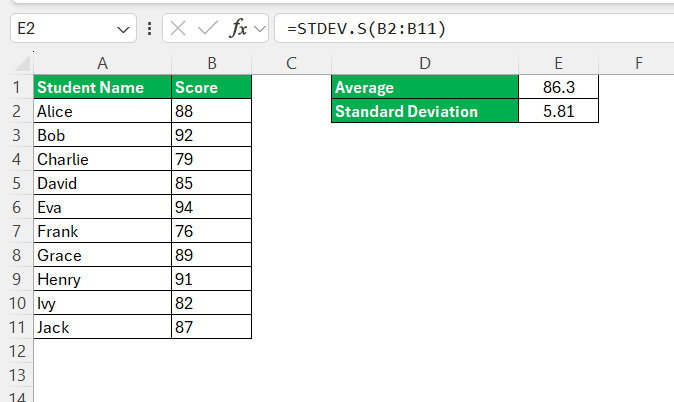
STEP 3: Use the STDEV.S function (for a sample) or STDEV.P (for a population) to calculate the standard deviation.

STEP 4: Use the COUNT function to find the number of data points.

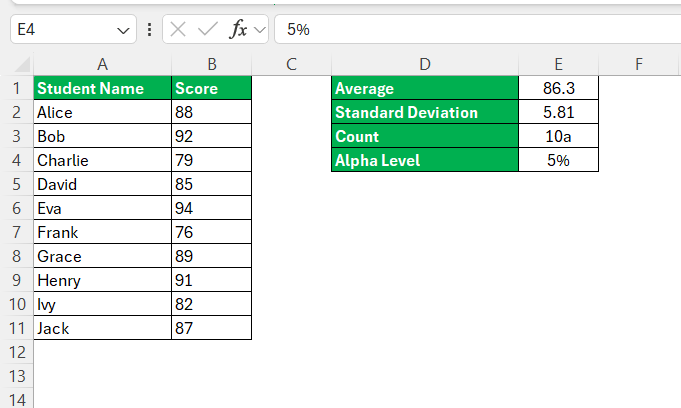
STEP 5: For a 95% confidence interval, the confidence level is 0.95. The alpha (α) level, which is 1 – confidence level, would be 0.05.

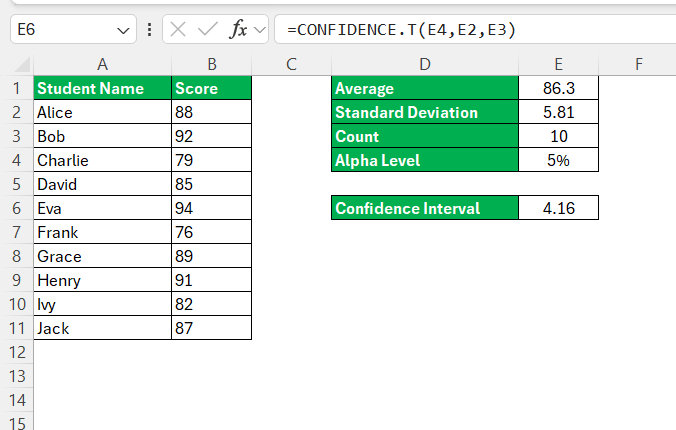
STEP 6: Enter the Confidence function.

 

Fix Common Errors

• The standard deviation should be greater than 0.
• There should be more than 1 sample of data.
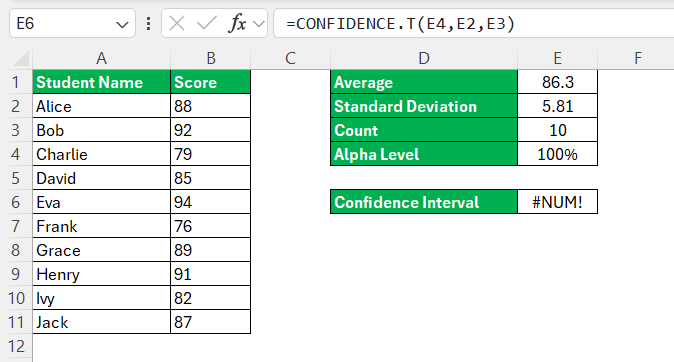
• Make sure that the value of alpha is between 0 and 1, not inclusive.

• All inputs should be numeric. Any non-numeric input will result in #VALUE! error.

• There should be no hidden characters in the data.

 

FAQs

Which confidence interval function should you use?

Follow this guideline when selecting the CONFIDENCE interval formula:

• Use the CONFIDENCE.T formula – When the sample size is small, and the population standard deviation is unknown.
• Use the CONFIDENCE.NORM formula – When the sample size is large, and the population standard deviation is known.

How to Select the Right Alpha Value?

Choosing the right alpha value for your confidence interval depends on your required confidence level. It is calculated as 1 minus the confidence level. For a 95% confidence interval, the alpha would be 0.05.

How to Calculate Multiple Confidence Intervals?

You can apply the CONFIDENCE formula to a cell. Then, drag the formula down to copy it across other ranges of cells.

How to calculate 95% confidence interval in Excel?

Follow the steps below to calculate 95% confidence interval in Excel:

• Use the AVERAGE formula to calculate the mean.
• Use STDEV.P to calculate the standard deviation.
• Use the COUNT function to get the total number of observations.
• Alpha will be 0.05 as the confidence level is 95%.
• Enter the formula: =CONFIDENCE(alpha, standard deviation, count)