Continuously Compound Interest Formula in Excel

When I first started diving into financial calculations in Excel, one concept that caught my attention was continuously compound interest formula. It’s a fascinating formula used in finance and investing, and Excel makes it surprisingly simple to compute. Let me walk you through how to calculate it step-by-step.

Key Takeaways:

• Continuous compounding grows investments faster than periodic compounding by accruing interest non-stop.
• Excel simplifies continuous compounding with the formula =PEXP(rt), allowing dynamic financial calculations.
• Key formula elements include principal (P), rate (r), time (t), and Euler’s number (e ≈ 2.71828).
• Continuous compounding is useful for modeling theoretical growth benchmarks in finance.
• Accurate inputs and proficiency with formulas ensure reliable Excel calculations for financial analysis.

 

Introduction to Continuous Compounding in Excel

Understanding the Power of Compound Interest

Albert Einstein may well have called compound interest one of the world’s wonders, and not without reason. The concept allows us to grasp a financial phenomenon where our wealth doesn’t just grow, it multiplies over time. Compound interest is one of the most powerful concepts in finance. With the right formulas and a little patience, you can see your investment grow exponentially over time.

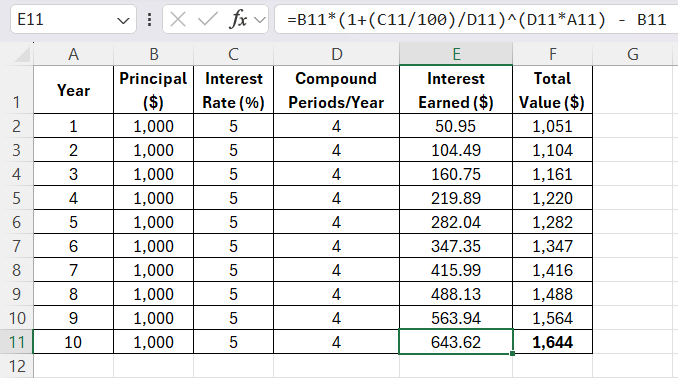
After 10 years, your $1,000 investment at 5% annual interest, compounded quarterly, would grow to $1,643.63, which means you’ve earned $643.63 in interest over that period.

This example demonstrates the exponential nature of compound interest — the longer your money is invested and the more frequently it’s compounded, the more you earn!

 

Breaking Down the Continuous Compounding Formula

Core Components of the Formula

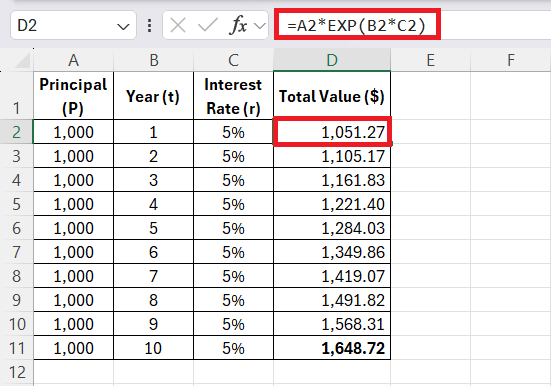
When I dive into the continuous compounding formula, it becomes clear that it’s built on a backbone of several core components. The formula, expressed as A = Pe^(rt), succinctly represents how an investment grows over time with continuous interest.

Here’s what each symbol stands for:

• ‘A’ is the amount of money accumulated after n periods, including interest.
• ‘P’ is the principal amount (the initial sum of money).
• ‘e’ is Euler’s number (approximately 2.71828), the base of natural logarithms.
• ‘r’ is the annual interest rate (in decimal).
• ‘t’ is the time the money is invested for, in years.

This equation showcases the exponential growth of an investment year on year, taking into account non-stop interest accrual. The principal ‘P’ bears the potential ‘seeds’ of growth, ‘r’ shapes the rate at which the investment will swell, and ‘t’ indicates the investment horizon. Meanwhile, Euler’s number ‘e’ acts as a growth constant, ensuring that all this occurs continuously.

For my investment scenario, I had the following key details:

• Principal (P): This is the initial amount of money I invested, which was $1,000. I wasn’t adding any more money after this initial investment.
• Interest Rate (r): The annual interest rate is 5%. This means that, every year, the account earns 5% of its value as interest.
• Compounding Frequency (n): This is how often the interest is added to the account each year. In my case, the interest was compounded quarterly, meaning 4 times per year.
• Time (t): The investment would be tracked over 10 years to see how the money grows.

With these variables in mind, the compound interest formula helps us calculate how much the investment will be worth after 10 years, taking into account the effect of compounding. Now that I had the understanding of the formula, it was time to implement it in Excel. Here’s how I did it step-by-step:

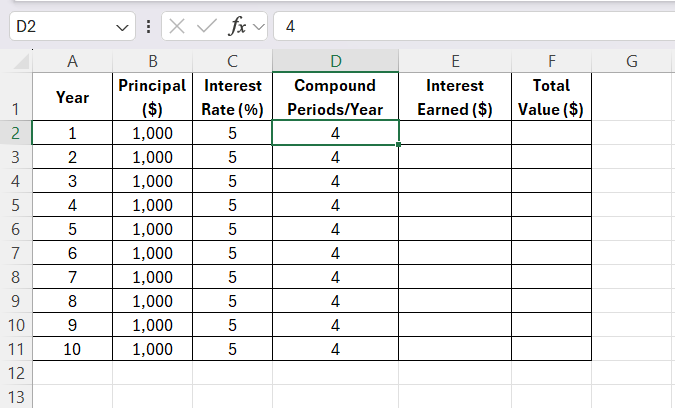
STEP 1: Setting Up My Excel Sheet

Now that I understood the formula, I wanted to see how my $1,000 investment would grow over 10 years in an easy-to-read format. So, I set up an Excel spreadsheet with the following columns:

Here’s how I populated the columns:

• Year: I entered the years from 1 to 10.
• Principal: For each year, I set the principal amount to $1,000 (since I’m not adding additional money during this period).
• Interest Rate: I entered 5% for the interest rate.
• Compound Periods/Year: I entered 4 because the interest compounds quarterly.
• Interest Earned and Total Value: These columns would be calculated using the compound interest formula.

STEP 2: Applying the Compound Interest Formula

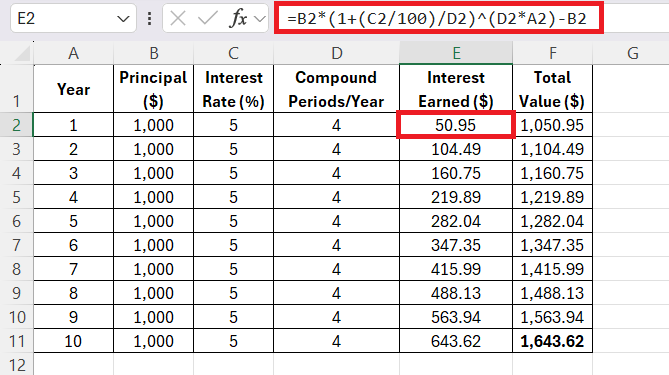
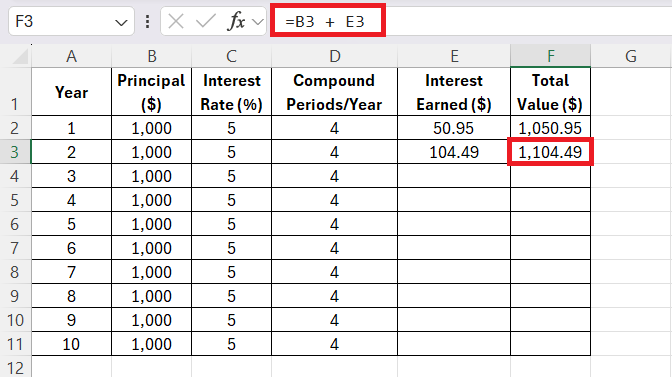
With the spreadsheet set up, it was time to calculate the growth of my investment. I used the compound interest formula directly in Excel. The formula I used for the Interest Earned in Year 1 was:

“=B2*(1+(C2/100)/D2)^(D2*A2)-B2”

This formula calculates the Interest Earned by subtracting the original principal from the final value of the investment.

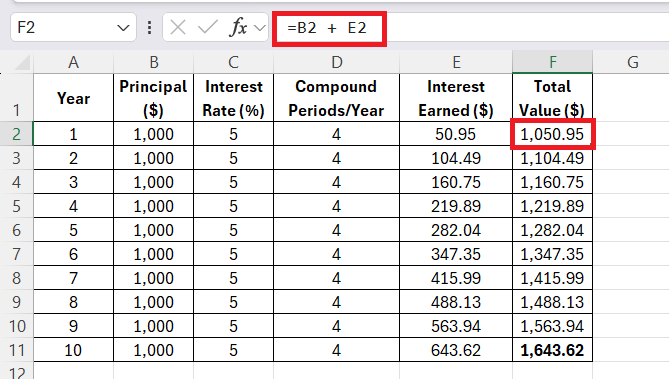
STEP 3: After that, I added the interest earned to the Principal to get the Total Value.

STEP 4: Copying the Formula for the Following Years

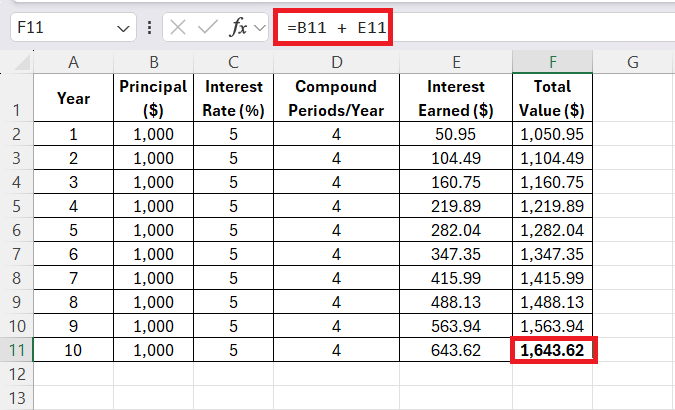
Once I had calculated the first year’s values, I copied the same formulas down the columns for the remaining years. This allowed Excel to automatically calculate the Interest Earned and Total Value for each subsequent year, based on the same interest rate and compounding frequency.

STEP 5: Reviewing the 10-Year Growth

I continued this process for all 10 years, allowing the power of compound interest to work its magic. By Year 10, my $1,000 investment had grown to:

Over the 10 years, the total value of your initial $1,000 investment grows to $1,643.62, with a total interest earned of $643.62.

Automating continuous compounding Calculations with the Excel Formula

With my data ready and waiting, I pivot to automating the magic of compound interest. Excel simplifies this task with its formula functions. Instead of grappling with math each time, I create a formula once and watch it work its wonders as I plug in different numbers.

In continuous compounding, the interest accrues non-stop, growing more rapidly than in periodic compounding because interest is calculated continuously and applied to the growing total at every infinitesimal moment.

For continuous compounding, I employ formula =PEXP(rt), replacing P, r, and t with references to the cells where my principal, rate, and time reside. With each change in input data, Excel recalculates the future value of the investment instantaneously. It’s a dynamic and responsive way to model financial scenarios, shaving hours off of complex calculations.

 

The Real-world Impact of Continuous Compounding

How Continuous Compounding Influences Financial Strategies

Continuous compounding has a subtle yet potent influence on financial strategies, particularly in the realms of investment and corporate finance. By understanding the theoretical maximum of growth potential for investments, I gain a benchmark against which to gauge actual performance and decision-making.

Financial managers can use continuous compounding to compare funding options, which impacts strategic moves such as business expansion or product development. This knowledge can alter the risk-reward calculus, shaping not just the choice of investment vehicles but also the timing and scale of investments.

Recognizing the Limitations of Excel in Complex Scenarios

While Excel is an exceptionally powerful tool for financial analysis, it’s important to recognize its limitations, especially in exceedingly complex scenarios. Excel performs optimally within the bounds of its built-in functions and the correct application of formulas, but it might not be equipped to tackle highly specialized financial simulations or scenarios involving stochastic elements without additional plugins or custom code.

Furthermore, when the datasets grow extremely large or when real-time collaboration is crucial, alternative data processing tools or business intelligence software might be more efficient. It’s also essential to remember that the accuracy of Excel’s complex financial models hinges on user proficiency, the integrity of input data, and the understanding of underlying financial concepts.

 

 

FAQ on Continuously Compounding Interest in Excel

How do you continuously compound interest in Excel?

To calculate continuously compounded interest in Excel, first input your principal amount (P), interest rate (r), and time in years (t). Then, use the formula =PEXP(rt) in a cell. Replace P, r, and t with cell references to automatically compute the accumulated amount.

How Accurate is Excel’s Continuous Compounding Formula?

Excel’s continuous compounding formula is considerably accurate for the theoretical model it represents. Given correct inputs and proper formula application, the results are reliably precise. However, real-world factors may introduce variability not captured by the model.

Can Continuous Compounding be Applied to All Investment Types?

Continuous compounding can be applied to various investment types, but its benefits are more pronounced over longer durations. It’s particularly relevant for instruments where interest can be reinvested at very frequent intervals. However, not all investments cater to this kind of compounding.

What are the Common Errors to Watch Out for When Using Excel Formulas?

When using Excel formulas, common errors include incorrect cell references, typos in formulas, and mismatching date formats or units. Also, forgetting to fix the reference cell with the dollar sign ($) can lead to incorrect copying of formulas. Double-check your work to avoid these pitfalls.

Is Excel’s Continuous Compounding Formula Applicable for Short-term Investments?

Excel’s continuous compounding formula can be used for short-term investments, but the difference between continuous and regular compounding is minimal over short periods. For brief investment horizons, traditional compounding methods may be more practical and yield similar results.