If you’re exploring trigonometric functions in Excel, the COSH function can be incredibly helpful for calculating the hyperbolic cosine of a given number. It might sound complex, but don’t worry—I’ll walk you through each step to show you just how straightforward it can be to use the COSH function for your calculations.
Key Takeaways:
- The COSH function in Excel calculates the hyperbolic cosine, useful for exponential and hyperbolic modeling in fields like physics and finance.
- COSH requires only one input parameter, making it straightforward to use in more complex formulas.
- This function helps model exponential growth, decay, and volatility in diverse areas, including stock market and loan analysis.
- COSH can be paired with functions like SUM and AVERAGE to gain deeper insights in engineering or financial data.
- Ensure numerical inputs to avoid #VALUE! errors, and use Excel’s manual calculation mode for large datasets.
Table of Contents
Introduction to COSH Function
What is the COSH Function?
The COSH function is an invaluable tool for professionals who frequently engage with mathematical and trigonometric formulas in their work. Specifically, it computes the hyperbolic cosine of a number—a function akin to the well-known cosine in trigonometry but more suited for hyperbolic rather than circular relationships.
Hyperbolic functions like COSH find applications across a range of fields, from finance to engineering, where they might be used to model growth or describe the shape of waves.
The Importance of Hyperbolic Functions in Excel
As I’ve delved into various analytical tasks, I’ve recognized the indispensable role hyperbolic functions play in Excel. In different fields such as physics, finance, and engineering, these functions, including COSH, provide a remarkable ability to model systems with exponential growth or decay, and oscillations.
For example, analyzing the propagation of waves or predicting the growth of investments can be accurately executed using hyperbolic functions. They enable a deep and precise analysis which could not be as easily replicated by using ordinary trigonometric or linear functions.
In essence, the addition of hyperbolic functions enriches our analytical toolbox within Excel, presenting us with the capabilities to explore and model complex, real-world scenarios effectively.
Getting Started with COSH
Understanding the Syntax of COSH
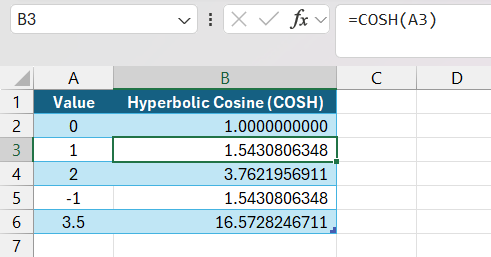
Grasping the syntax of the COSH function in Excel is straightforward and doesn’t require intricate knowledge of mathematics. The syntax is simply =COSH(number), where “number” is the argument for which you want to find the hyperbolic cosine. To get the outcome, I performed these steps:
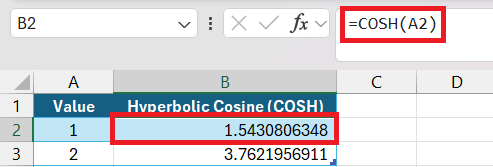
STEP 1: Entered the value data in Column A. Then select the desired cell where I wanted to find the Hyperbolic Cosine.
STEP 2: Enter the formula “=COSH(A2)” for this example.
In practice, this might be a manual entry, a cell reference, or even a result from a different formula or function. Unlike some other functions in Excel, COSH is uncomplicated, with only one input parameter to manage, making it painless to integrate into more complex equations and analyses.
Input Parameters and Their Significance
When we work with the COSH function, there’s just one input parameter to consider, which is both a relief and an efficiency booster. This parameter is the numerical value for which we’re calculating the hyperbolic cosine.
It’s vital to understand this parameter can be any real number—negative, positive, or zero—which offers broad flexibility. The significance of this single parameter lies in its representation of an angle in hyperbolic space, similar to how we think of angles in a circle for trigonometric cosine.
This fundamental input sets the COSH function into motion, enabling a vast array of mathematical modeling and analyses within Excel.
Practical Examples of COSH Function Usage
Analyzing Stock Market Data with COSH
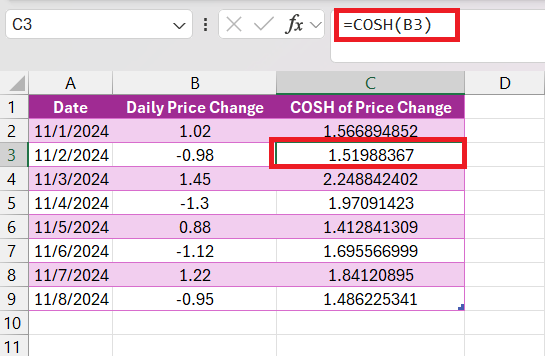
Analyzing stock market data with the COSH function can be quite enlightening, especially when it comes to examining volatility and price trends. By inputting daily price changes into the COSH function, I can calculate the hyperbolic cosine of these changes – a method that can provide unconventional yet insightful perspectives on market behavior.
While it won’t give you buy or sell signals, it can help in smoothing out data to understand underlying trends, much like other transformation functions used in financial analysis.
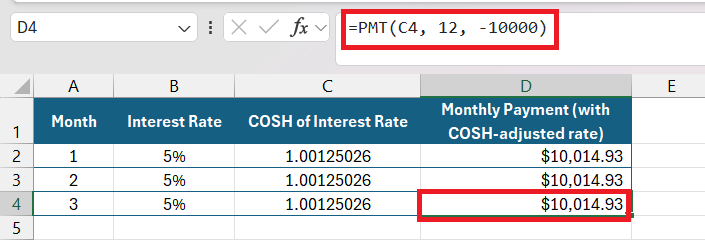
Calculating Loan Payments Using COSH
When calculating loan payments, the COSH function offers a novel approach. By representing the interest rate with the COSH function, I can provide a clear, albeit unconventional, perspective on the cost of a loan.
While this is not a standard method for calculating loan payments (more frequently handled by functions like PMT), using COSH can give me a unique view of how interest rates might impact payments on a more hyperbolic scale, particularly useful in complex financial models or where compounded interest rates behave non-linearly.
Advanced Tips for Excel Users
Integrating COSH with Other Formulas
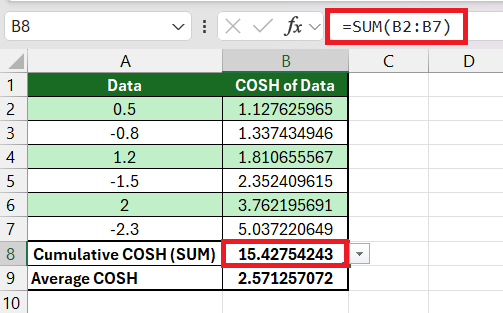
Integrating the COSH function with other formulas can elevate data analysis to a new tier. For instance, I often combine COSH with statistical functions like AVERAGE or SUM to investigate datasets in more depth.
Combining COSH with SUM, for example, allows me to evaluate the cumulative hyperbolic cosine values for a series, which can be particularly interesting in financial or engineering data that exhibits exponential characteristics.
Pairing it with AVERAGE, I can discern the average hyperbolic cosine, providing a central tendency measure for data sets where COSH is applicable.
Troubleshooting Common Issues with COSH
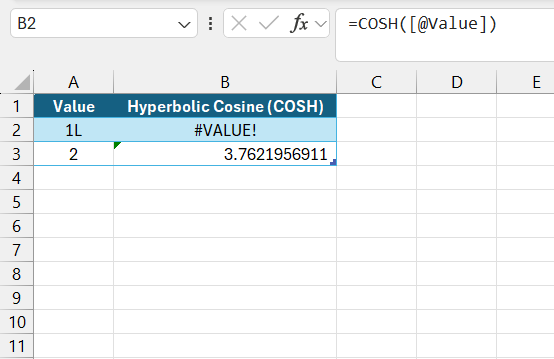
Troubleshooting is part and parcel of working with functions like COSH. Sometimes you might run into #VALUE! errors, often indicating that the input isn’t recognized as a numerical value. It’s a cue to double-check the data entry for accuracy.
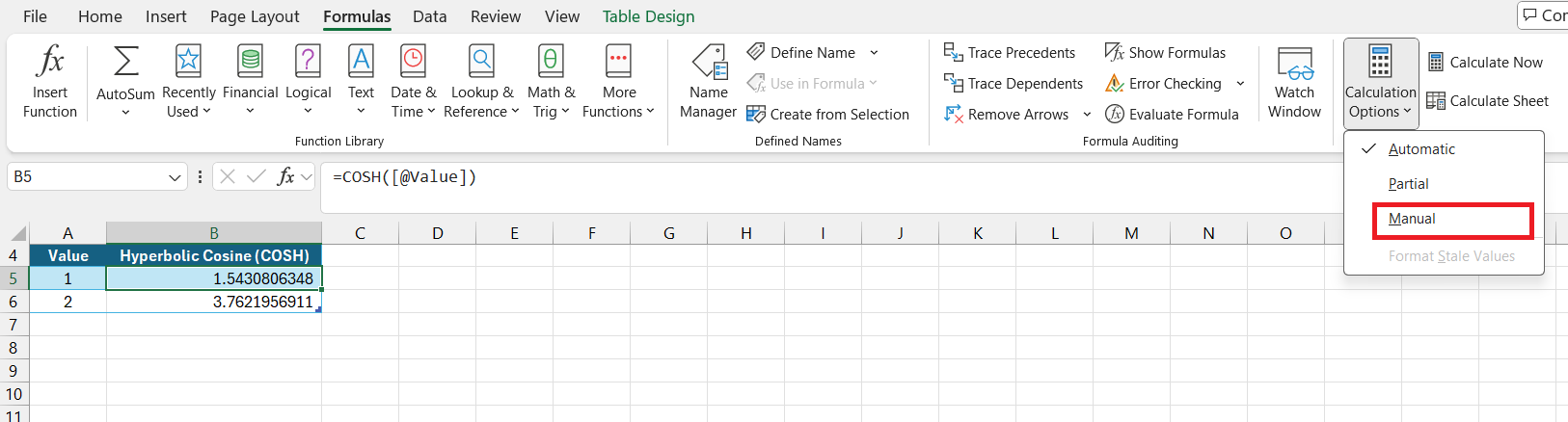
Additionally, if the results seem out of order, I make sure that all input numbers and formulas are correctly entered, since typos can disrupt the entire calculation. For performance issues with large datasets, I utilize Excel’s manual calculation mode or optimize formulas to improve efficiency.
These steps usually remedy the most prevalent issues, ensuring a smooth operation when using COSH.
FAQ Section
What is the formula for cosh?
The formula for calculating the hyperbolic cosine (COSH) is COSH(z) = (e^z + e^(-z)) / 2, where ‘e’ is the base of the natural logarithm, and ‘z’ is the number or angle in hyperbolic space for which the hyperbolic cosine is being calculated.
How to use cosh function in Excel?
To use the COSH function in Excel, simply type =COSH(X) into a cell, replacing X with the number you want to calculate the hyperbolic cosine for, or with a reference to a cell containing the numeric value. Press Enter, and Excel displays the COSH of the given number.
How Does COSH Differ from Traditional Trigonometric Functions?
COSH differs from traditional trigonometric functions in that it corresponds to hyperbolic rather than circular geometry. Whereas functions like cosine deal with circular angles, COSH involves hyperbolic angles, describing shapes like hyperbolas. These hyperbolic functions exhibit exponential growth, unlike the periodic sine and cosine functions that oscillate between fixed values. This distinctive behavior makes COSH suitable for different types of data analysis and modeling, particularly where exponential growth or decay is observed.
Can COSH be Used for Non-Financial Data Analysis?
Absolutely, the COSH function can be utilized for non-financial data analysis too. It’s particularly valuable in engineering and physics, for instance, where it can help model the shape of a cable suspended under its own weight or represent waveform characteristics. Apart from scientific applications, it can also be leveraged in other domains like data science for smoothing or transforming datasets, making COSH a versatile tool across various fields that require the handling of exponential and hyperbolic relationships.
What are Some Common Mistakes to Avoid When Using COSH Function?
When using the COSH function, some common pitfalls include expecting negative results—COSH always returns positive values. It’s also essential to use appropriate inputs since incorrect numbers can skew the model or analysis. And when dealing with multiple cells, don’t forget to autofill the formula to ensure all calculations are updated—this simple step can save time and prevent errors. By staying mindful of these aspects, I can maintain data integrity and reliability in my analysis.
John Michaloudis is a former accountant and finance analyst at General Electric, a Microsoft MVP since 2020, an Amazon #1 bestselling author of 4 Microsoft Excel books and teacher of Microsoft Excel & Office over at his flagship MyExcelOnline Academy Online Course.