The Ultimate Guide to Cotangent Formula in Excel

When I first started using Excel for mathematical calculations, I was thrilled by its ability to handle complex formulas and functions effortlessly. One such formula that caught my attention was the cotangent formula. If you’re exploring trigonometric functions in Excel, understanding how to calculate cotangent can be a game-changer. Let me walk you through everything you need to know about using the cotangent formula in Excel.

Key Takeaways:

• The COT function in Excel calculates the cotangent of angles in radians, making it essential for trigonometric tasks.
• Always convert degrees to radians before using the COT function, either with the RADIANS function or manual multiplication by PI()/180.
• You can sum or average cotangents using Excel functions like SUM and AVERAGE for advanced analysis.
• The COT function integrates seamlessly with other trigonometric functions like SIN, COS, TAN, and ATAN for complex calculations.
• Non-numeric inputs for the COT function result in a #VALUE! error, highlighting the importance of providing valid numeric angles.

 

Simplifying the Cotangent Function in Excel

Demystifying the COT Formula

Excel is a powerful tool that wields a multitude of functions, one of which is the trigonometric COT function. At first glance, it may seem daunting, but it’s quite straightforward once we break it down. Think of COT as a translation service; it converts angles into cotangents, an essential trigonometric ratio.

 

Crafting the Perfect Cotangent Formulas

Basic Syntax: Understanding the COT Function

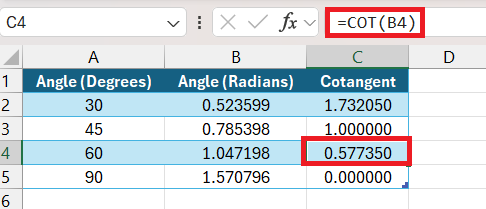
Understanding the COT function in Excel is essential for performing trigonometric or geometric calculations. At its core, the COT function simplifies the process of finding the reciprocal of the tangent of an angle, which is the cotangent.

Here’s the basic syntax:

=COT(number)

Where number is the angle in radians for which you want the cotangent.

Let’s look at an example to make this clear and practical.

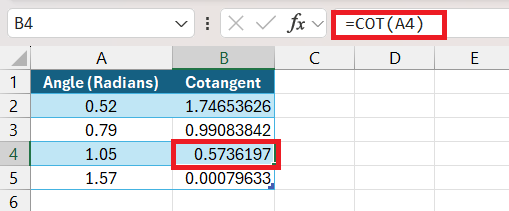
Real-Life Example: Calculating the Cotangent of Angles in Radians

Imagine you’re designing a ramp and need to calculate the slope’s cotangent for various angles. The angles are already measured in radians, and you’ll use the COT function to find their cotangents.

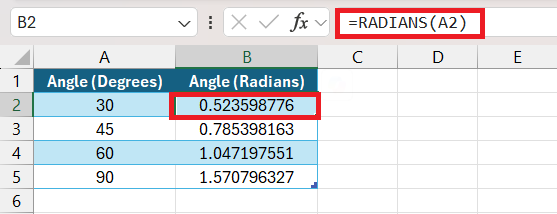
Don’t forget, if your angles are in degrees, we need to convert them to radians first using the RADIANS function. It’s like ensuring we’re speaking the same language as Excel before asking it to perform its magic. With consistent syntax and understanding of radians, the COT function is a breeze to use.

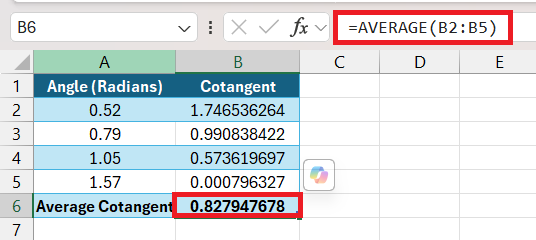
Advanced Uses: Summing and Averaging Cotangents

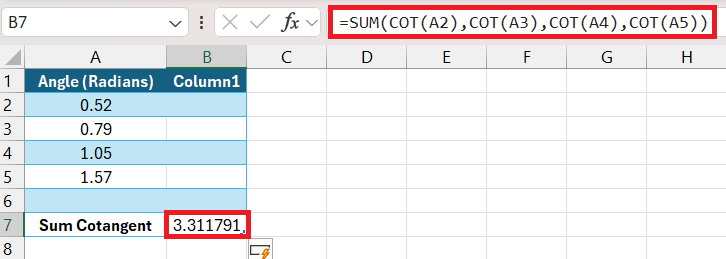
When we’ve mastered the COT on its own, summing and averaging cotangents is just a step further in our Excel journey. These advanced operations allow us to analyze a set of angles collectively, giving us more insight than individual cotangent values can provide.

For summing cotangents, we enlist the SUM function joined with multiple COT functions, like this: =SUM(COT(angle1), COT(angle2), …), where ‘angle1’, ‘angle2’, etc., are the angles in radians. We’re asking Excel to calculate the cotangent of each angle separately and then sum them all up.

As for averaging, we use the AVERAGE function in tandem with COT: =AVERAGE(COT(range_of_angles)). This request is like asking for a consensus among cotangents, giving us the arithmetic mean of these values over the range of angles provided. Both methods extend the COT function’s utility, offering us a broader statistical comprehension of our trigonometric data.

 

Real-World Applications

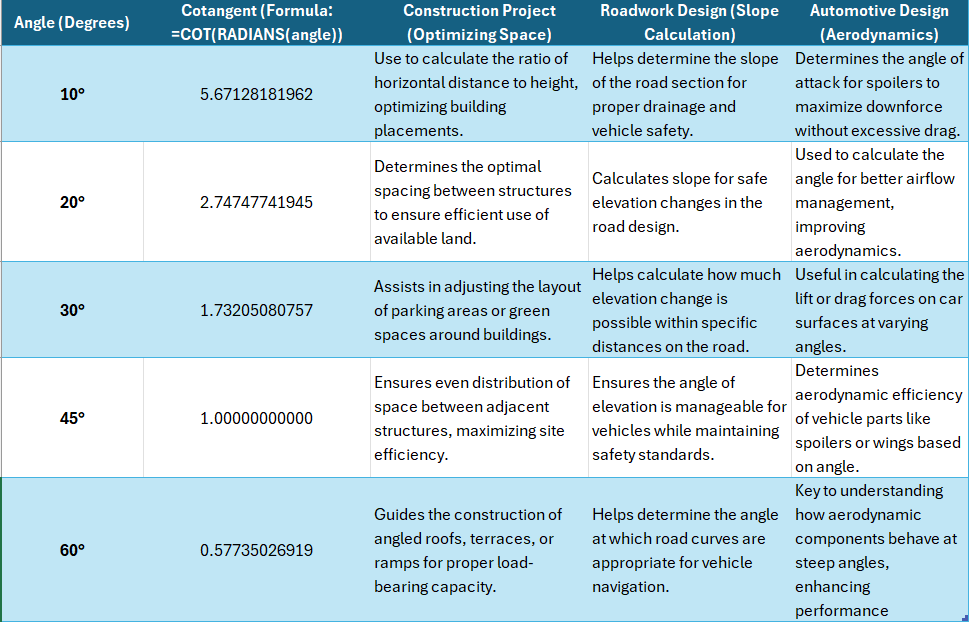
Project Management Wonders with Cotangent Calculations

In project management, leveraging cotangent calculations can work wonders in areas requiring spatial efficiency and resource optimization. Imagine you’re plotting the layout of a new construction site; by employing the cotangent of specified angles, you are able to optimize the use of space, ensuring that each structure perfectly complements its surroundings. It’s like piecing together a complex jigsaw puzzle with mathematical precision.

Additionally, cotangents assist in calculating slopes and angles in project designs, which can prove crucial in infrastructure projects like roadwork or aerodynamics in automotive design. It aids in making sure that real-world outcomes align with theoretical design, ensuring that projects are not only feasible but also executed with accuracy and efficiency.

 

Enhancing Your Excel Experience

The Seamless Connection Between COT and Related Functions

There’s a seamless connection between the COT function and its trigonometric counterparts in Excel — like SIN, COS, TAN, and ATAN — which all play in perfect harmony. This synergy allows us to venture into more complex trigonometric computations, where one function might complement another. For example, while COT offers the cotangent of an angle, ATAN provides the inverse, allowing us to reverse-engineer an angle from a cotangent value.

Incorporating related functions can enrich data analysis exponentially. By utilizing these functions together, we can solve for one trigonometric value using another, or convert between different forms of measurements. Combining them opens doors to sophisticated calculations, which are especially crucial in fields such as physics, engineering, and architecture.

Understanding this interconnectivity deepens our appreciation of Excel’s trigonometric powers, as each function harmoniously contributes to the suite of tools at our disposal for in-depth analytical work. By mastering these connections, we turn complex tasks into streamlined operations.

 

FAQ

Can I use degrees instead of radians with the COT function?

No, the COT function in Excel does not directly accept degrees; it requires angles in radians. To convert degrees to radians, use the RADIANS function or multiply the degree value by PI()/180 before passing it to the COT function. For example, use =COT(RADIANS(45)) or =COT(45*PI()/180) to find the cotangent of a 45-degree angle.

How do I calculate the average cotangent for multiple angles?

To calculate the average cotangent for multiple angles, use the AVERAGE and COT functions together. First, determine the cotangent of each angle using the COT function, and then average those results with the AVERAGE function. The formula looks like this: =AVERAGE(COT(angle1), COT(angle2), …), where angle1, angle2, etc., are your angles in radians.

What is the error value returned when the input is non-numeric?

When the input is non-numeric and you attempt to use the COT function in Excel, it returns the #VALUE! error. This error indicates that the input provided cannot be understood or processed by the function as it expects a numerical value representing an angle in radians.

How do I insert a COT in Excel?

To insert a COT function in Excel, click on the cell where you want the result, type =COT(), and inside the parentheses, input the angle in radians or a reference to the cell containing the angle. For example, you could type =COT(A1) if cell A1 has the angle in radians, then press Enter. Excel will display the cotangent of the entered angle.

What is the Acot function in Excel?

The ACOT function in Excel returns the arccotangent, or inverse cotangent, of a number, which is the angle in radians whose cotangent is that number. In simpler terms, if you have a cotangent value and you want to find the original angle in radians, you’d use the ACOT function. For example, =ACOT(1) will give you the angle in radians whose cotangent is 1, which is 0.785398163 radians.