The Ultimate Guide to CSC Function in Excel

When working with trigonometric calculations in Excel, I often find myself needing functions that go beyond the basics. While Excel provides sine, cosine, and tangent functions out of the box, there are times when I need the reciprocal of these values, like cosecant (CSC). I’ll show you how I calculate the cosecant of an angle using Excel’s CSC function.

Key Takeaways:

• The CSC function in Excel calculates the cosecant of an angle provided in radians, which is the reciprocal of sine.
• Always convert degrees to radians using the RADIANS function or manual conversion to ensure accurate results.
• Combine CSC with other Excel functions, like AVERAGE or IF, to enhance data analysis and streamline complex calculations.
• Check for errors like #DIV/0! when the sine of the angle is zero or ensure the input is numeric and in the correct format.
• Proper spreadsheet setup, including data validation and consistent formulas, ensures smoother calculations and minimizes errors.

 

Introduction to the CSC Function in Excel

What is the CSC Function?

The CSC function in Excel is a trigonometric utility that calculates the cosecant of an angle provided in radians. For those of us who might have a hazy memory of high school math, in trigonometry, cosecant is the reciprocal of the sine function.

This means it is expressed as 1 divided by the sine of the angle, or more formally, the length of the hypotenuse divided by the length of the opposite side in a right-angled triangle. The CSC function returns a numeric value that can be integral in diverse calculations involving angles.

The Importance of Trigonometric Functions in Excel

Trigonometric functions in Excel, such as the CSC function, are instrumental for a multitude of tasks that involve geometry and angles. From the realms of engineering to finance, and especially in the fields of science and data analysis, knowing how to utilize these functions allows for precise computations.

For instance, they’re useful when dealing with periodic data, such as waves or oscillations, where angles and their trigonometric properties are crucial. Additionally, they serve to solve architectural designs and other spatial problems that require a mathematical approach.

In the intricate web of Excel’s capabilities, integrating trigonometric functions can significantly enhance the way we interpret and model information. It allows us to move from simple data entry to complex, analytical problem-solving. The ability to execute these functions seamlessly within Excel broadens the application of spreadsheets making them a powerful tool in many professional fields.

 

Getting Started with the CSC Function

Understanding the Syntax and Parameters

The CSC function’s syntax is straightforward and easy to understand, consisting of a single argument. The required argument is number, which represents the angle in radians for which we want to calculate the cosecant.

Therefore, the complete function appears as CSC(number). It’s essential to ensure that the angle is provided in radians, as inputting degrees without conversion will yield incorrect results.

One thing to remember is that the number parameter cannot be a text value, and the angle must be a numeric value. If an angle is provided in degrees, it needs to be converted to radians first, which can be accomplished using Excel’s RADIANS function. If the angle is already in radians, it is simply entered as the number argument, and Excel will do the rest, retrieving the cosecant of the given angle.

 

How to Use the CSC Function

Basic Example

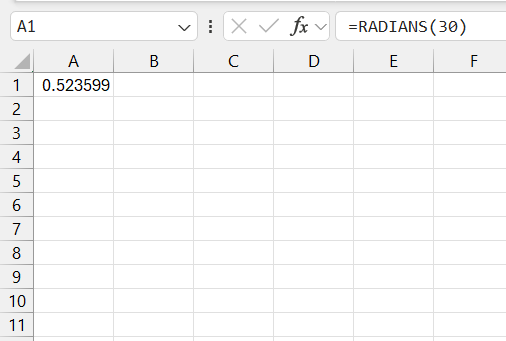
Suppose I have an angle of 30 degrees, and I want to find its cosecant. Since the CSC function requires radians, I’ll first convert 30 degrees into radians:

=RADIANS(30)

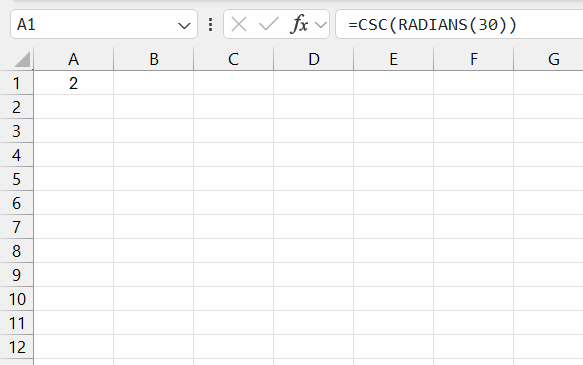
The result will be 0.523. Now, I use the CSC function:

=CSC(RADIANS(30))

The output is approximately 2.0.

Using CSC with Cell References

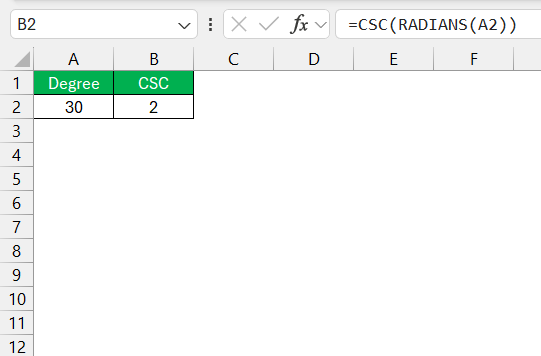
In practice, I often store my angles in cells to make calculations dynamic. Let’s say cell A2 contains the angle in degrees. To find the cosecant:

=CSC(RADIANS(A2))

This way, if the value in A2 changes, the result updates automatically.

 

Practical Tips for Using the CSC Function

Converting Degrees to Radians for Accurate Results

It’s paramount to convert degrees to radians when using trigonometric functions in Excel for accurate results, as these functions inherently expect radians. Not doing so can lead to incorrect calculations, which could have a domino effect on subsequent data analysis or decision-making.

Fortunately, the conversion process is simple in Excel. You can multiply the degree value by PI()/180, or you can use the built-in RADIANS function for a cleaner approach. To convert an angle in degrees to radians, use the RADIANS function like so:

=RADIANS(degree_value)

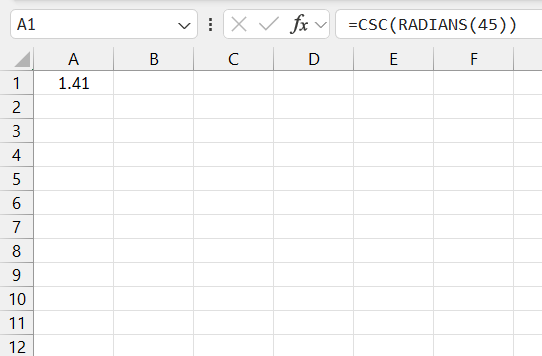
For a practical example, suppose you have an angle of 45 degrees that you want to use with the CSC function. You would write the formula as follows:

=CSC(RADIANS(45))

This small step ensures that the trigonometric function processes the angle correctly, delivering the accurate result you need for your calculations. Whether you’re working with a single value or an entire dataset, consistently converting degrees to radians is essential for maintaining the integrity of your Excel work.

Integrating the CSC Function with Other Excel Tools

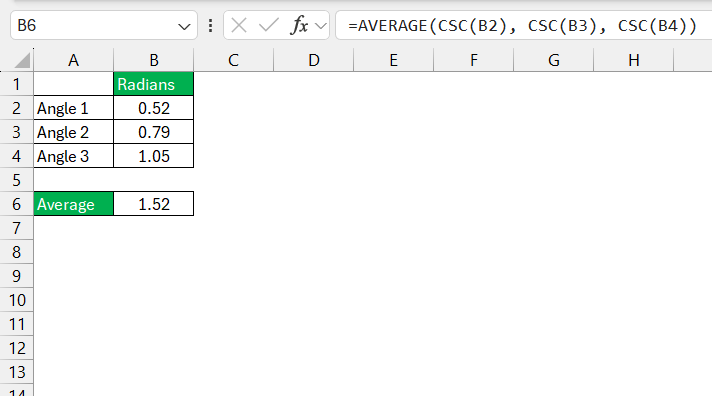
Integrating the CSC function with other Excel tools can elevate the complexity and depth of your analysis. Excel shines in its ability to mesh together various functions to achieve detailed and powerful results. For example, you might want to calculate the average cosecant value of an array of angles. This could be neatly executed by combining the CSC function with the AVERAGE function:

=AVERAGE(CSC(B2), CSC(B3), CSC(B4))

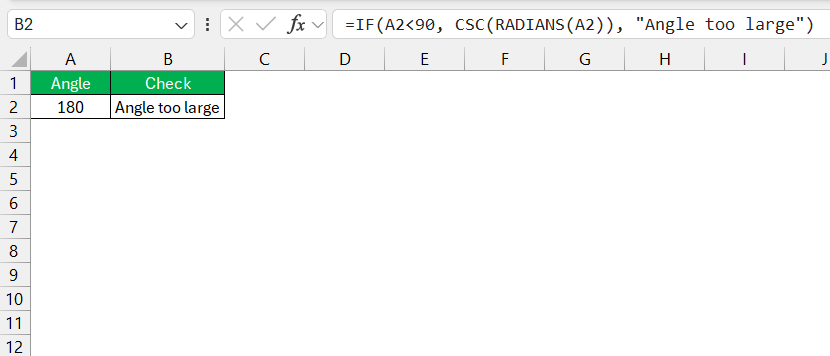
Now, this can be taken a step further by pairing it with statistical, lookup, or even conditional functions for more sophisticated operations. Imagine you need to compute the cosecant of an angle only if certain conditions are met, integrating IF statements with the CSC operation:

=IF(A2<90, CSC(RADIANS(A2)), "Angle too large")

By integrating the CSC function with other Excel tools, the possibilities become vast. It’s like piecing together a puzzle; the more functions you know how to interweave, the clearer the big picture becomes. As such, mastering the CSC function’s integrations is a step towards tapping into the full potential of Excel’s analytical power.

 

Troubleshooting Common CSC Function Errors

Why Your CSC Function Might Not Work and How to Fix It

If you find that your CSC function isn’t working as expected, don’t worry, you’re likely facing a common issue that can be remedied with some troubleshooting. Let’s explore the reasons and how to fix them.

Firstly, confirm that you’re using radians instead of degrees. Excel will give erroneous results for trigonometric functions if angles are not in radians. To fix this, use the RADIANS function to convert your degree values before feeding them into the CSC function.

Secondly, double-check your formula for syntax and parentheses. The structure of your function should look like =CSC(number) or =CSC(RADIANS(degree_value)). Ensure each opening parenthesis has a corresponding closing parenthesis.

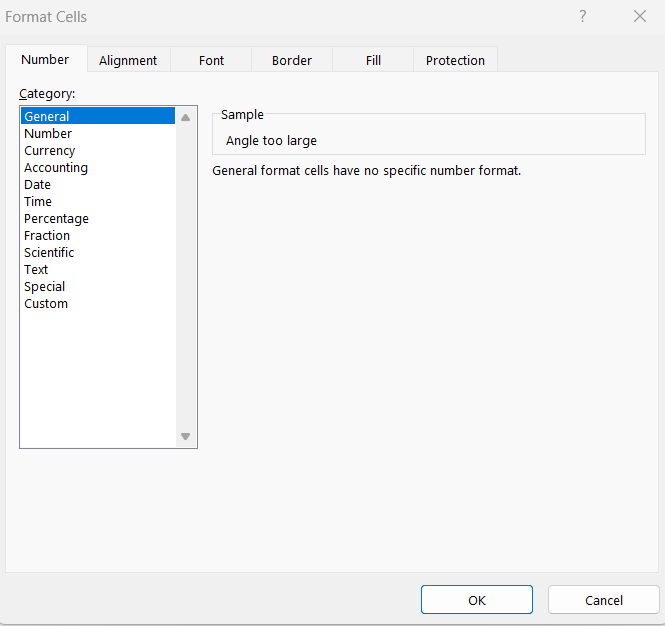
Also, make sure the cell containing the CSC function is set to the correct format. It should not be formatted as text, which would prevent Excel from recognizing it as a formula. You can check and change the cell formatting in the “Format Cells” dialog box.

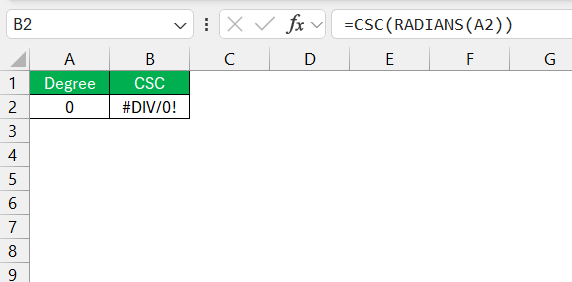
One more bit of advice: Watch out for the #DIV/0! error. This signals that the sine of the angle is zero, making the cosecant undefined. Adjust the input angle, so the sine isn’t zero.

Remember, attention to these details will resolve most issues with the CSC function, ensuring your calculations are accurate and reliable.

Avoiding Errors by Properly Setting Up Your Spreadsheet

To avoid errors when working with the CSC function or any formulas in Excel, proper spreadsheet setup is key. Begin by organizing your data logically and clearly, prefacing your calculations with data validation to prevent inappropriate values from being entered.

Use structured references like named ranges to make your formulas more readable and less prone to mistakes due to cell misreferences. For example, instead of using “B2”, name the cell “InputAngle” for clarity.

Set up data validation rules to ensure only valid inputs are accepted. For angles, this could mean restricting cell values to numeric entries and avoiding division by zero errors.

Next, use reliable error-checking features such as Excel’s “Error Checking” tool or formula auditing functionalities like “Trace Precedents” or “Trace Dependents” to track the flow of your formulas and spot potential errors due to incorrect cell references.

Keep your formulas consistent across cells by using absolute references where necessary. If your CSC function includes a cell that should not change as the formula is copied to other cells, make sure to anchor it with the dollar sign ($), like $B$2.

Lastly, always test your formulas to confirm they’re returning accurate results. Do this by performing spot checks with known values or by using a secondary method to calculate expected results.

A well-organized spreadsheet not only minimizes the potential for errors but also makes your work more efficient and less stressful.

 

FAQ: Mastering the CSC Function

What is the function of CSC ()?

The CSC() function in Excel computes the cosecant of an angle provided in radians. It’s a trigonometric function that’s essentially the reciprocal of the sine; for angle θ, CSC(θ) equals 1/sin(θ). It’s used in a variety of fields for calculating wave patterns, forces and angles in engineering, architectural designs, and even financial modeling.

How Do I Convert Angles from Degrees to Radians in Excel?

In Excel, to convert an angle from degrees to radians, use the RADIANS function. The formula looks like this: =RADIANS(degree_value). Replace degree_value with the angle in degrees, you wish to convert, and Excel will provide you with the corresponding value in radians.

Can the CSC Function Be Used in Combination with Other Functions?

Yes, the CSC function can be effectively combined with other functions in Excel to accomplish more complex tasks. You can use it alongside statistical functions like AVERAGE, or within conditional statements like IF, and many others to enhance data analysis and automate calculations involving trigonometric values.

Why isn’t my CSC working?

Your CSC function may not work for several reasons: you might be inputting degrees instead of radians—ensure you use RADIANS function for conversion; check for correct syntax and that the cell is formatted properly (not as text); and ensure parentheses are used correctly around the argument.