The Ultimate Guide to Euclidean Distance Calculator in Excel

Euclidean distance is a fundamental metric in various scientific and engineering fields, particularly in statistics, data analysis, and machine learning. It represents the straight-line distance between two points in Euclidean space. This article will guide you through the process step-by-step on how to use the Euclidean distance calculator in Microsoft Excel.

Key Takeaways:

• Euclidean distance measures the straight-line distance between points, vital in many scientific and engineering applications.
• Use Excel’s SUMXMY2 to compute squared differences and SQRT to find the distance.
• Arrange data in columns, apply SUMXMY2, and use SQRT for the final distance.
• Essential in data analysis, machine learning, physics, and computer graphics.

 

Understanding Euclidean Distance

The Euclidean distance between two points (1,1) and (2,2) in a 2-dimensional space is calculated using the formula:

Distance=SQRT((X2-X1)^2 + (Y2-Y1)^2)

For points in higher dimensions, the formula extends to:

Distance=SQRT((X2-X1)^2 + (Y2-Y1)^2)+….+(Z2-Z1)^2)

In Excel, you can calculate this distance for any number of dimensions using the SUMXMY2 and SQRT functions.

 

Using SUMXMY2 and SQRT Functions in Excel

The SUMXMY2 function in Excel calculates the sum of squares of differences between corresponding elements in two arrays. The syntax is:

=SUMXMY2(,)

This function will return the sum of squared differences. To get the Euclidean distance, you then need to take the square root of this sum using the SQRT function.

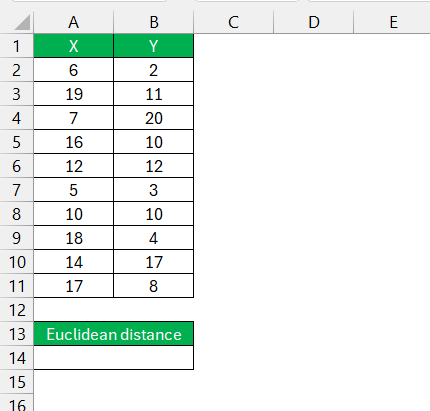
STEP 1: Arrange your data points in columns. For instance, if you have two points A and B with three dimensions, you might organize your Excel sheet as follows:

STEP 2: Calculate the Sum of Squared Differences –

• Use the SUMXMY2 function to calculate the sum of squared differences between the two points.
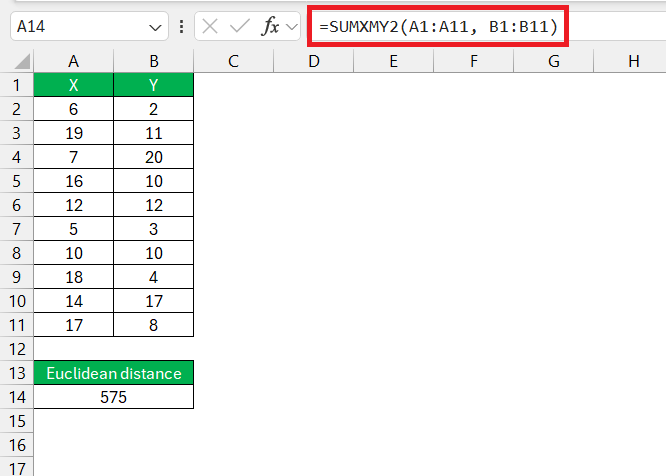
• Assume the data for point A is in cells A1:A11 and the data for point B is in cells B1:B11. In an empty cell, enter the formula:

=SUMXMY2(A1:A11, B1:B11)

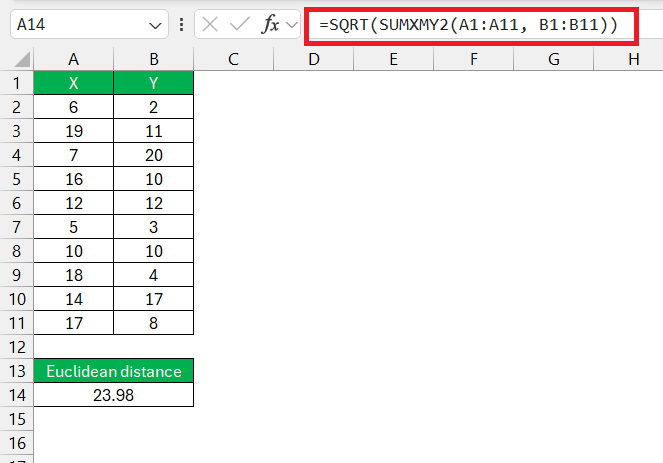
STEP 3: To get the Euclidean distance, take the square root of the result obtained from SUMXMY2.

=SQRT(SUMXMY2(A1:A11, B1:B11))

So, the Euclidean distance between points A and B is approximately 23.98.

 

Applications of Euclidean Distance Calculator

• Data Analysis and Machine Learning: Euclidean distance is used to measure similarity between data points. It is commonly used in clustering algorithms (e.g., k-means) and nearest neighbor search.
• Physics and Engineering: It helps in computing the distance between objects in space, crucial for trajectory calculations and spatial analysis.
• Computer Graphics: Used in rendering, animation, and image processing to calculate distances between pixels or objects.

 

Benefits of Using Excel for Euclidean Distance Calculations

• Accessibility and Ease of Use – Excel is widely accessible and user-friendly, making it an excellent tool for those who need to perform Euclidean distance calculations without learning complex programming languages.
• Built-in Functions – Excel’s built-in functions, such as SUMXMY2 and SQRT, simplify complex mathematical operations, making it easier to focus on data analysis rather than computation.
• Visualization Capabilities – Excel’s robust visualization tools allow users to plot data points and visually assess distances, providing an intuitive understanding of spatial relationships.
• Flexibility – Excel supports various data formats and can handle multiple dimensions, making it versatile for different applications, from simple 2D calculations to more complex multidimensional analyses.

 

Conclusion

By using Excel’s SUMXMY2 and SQRT functions, you can easily calculate the Euclidean distance between two points, regardless of the number of dimensions. This method is efficient and leverages Excel’s built-in functions to simplify complex mathematical calculations, making it accessible even for those with limited programming knowledge. Whether you’re working on a simple project or a complex data analysis task, this approach will help you compute distances accurately and efficiently.

 

FAQs

What is the Euclidean distance used for?

Euclidean distance is used in various fields to measure the straight-line distance between points. It’s particularly handy in areas like navigation systems, machine learning algorithms, computer graphics, spatial analysis, and clustering in data mining, amongst others. Essentially, it helps to quantify the similarity or divergence of data points in space.

How do I calculate the Euclidean distance between two points in Excel?

In Excel, calculate the Euclidean distance by inputting the coordinates into separate cells and applying the formula =SQRT((X2-X1)^2 + (Y2-Y1)^2). This will give you the distance between two points in a 2D space. For 3D, add (Z2-Z1)^2 within the square root.

Can the Euclidean distance be calculated between more than two points at once?

Yes, you can calculate the Euclidean distance between multiple points sequentially in Excel, but not all at once. You’ll measure the distance from one point to another, then move to the next pair, and so on.

Is Euclidean distance applicable in fields other than mathematics?

Absolutely, Euclidean distance finds applications in numerous fields apart from mathematics, such as computer science, physics, machine learning, biology, and economics, to name a few. It’s essential for tasks that involve spatial relationships or pattern recognition.

Are there alternatives to the Euclidean distance when measuring distances?

Indeed, there are multiple alternatives to the Euclidean distance for measuring distances, depending on the data and the context. The Manhattan distance measures the absolute sums of the differences and is used in grid-like path calculations. The Minkowski distance generalizes both Euclidean and Manhattan distances, allowing for flexibility in measurement. Each provides a different perspective on the concept of space and distance.