How to Use Excel Rate Function for Interest Calculations

Discover the financial crystal ball within Microsoft Excel‘s RATE function. It’s your guide to understanding interest rates for loans or investments, offering clarity for your financial future.

Key Takeaways:

• Foundational Finance: Interest calculations are fundamental to financial analysis, influencing decisions on loans, savings, and investments.
• Syntax Simplified: Understand the components of the RATE function, from periods to present value, in a straightforward syntax breakdown.
• Practical Application: Learn to use RATE with step-by-step examples, from calculating loan interest to determining savings growth.
• Troubleshooting Tips: Address common errors and ensure accurate results by troubleshooting issues like #NUM! and #VALUE! errors.
• Advanced Insights: Explore advanced applications, such as analyzing investment returns with precision and comparing RATE with related Excel tools.

 

Introduction to Excel’s RATE Function

Decoding the Basics of RATE Function

Imagine you’re holding the keys to better understanding your financial future. That’s what getting to grips with Excel’s RATE function offers you. Now, let’s demystify the basics; RATE is your go-to formula when you need to figure out the interest rate for loans or investments based on regular, consistent payments and a known timeframe.

You tell Excel what you’re aiming to achieve financially, and RATE spits out the periodic interest rate necessary to get there. It’s like a financial crystal ball in function form, helping you to plan ahead with clarity.

Importance of Interest Calculations in Financial Analysis

When it comes to the world of finance, the power of interest calculations cannot be overstated. They form the cornerstone of financial analysis, guiding decisions on loans, savings, and investments. Whether you’re angling to grow your nest egg or shave off costs on a mortgage, understanding how much money accumulates or what’s owed over time is vital.

It impacts everything from monthly payments to long-term financial goals. Using the RATE function in Excel, you unlock the ability to forecast these figures with precision, ensuring that every financial step taken is a calculated and informed one.

 

Understanding the Syntax of RATE Function

The RATE function in Excel calculates the interest rate per period of an annuity, given the number of periods, the payment per period, the present value (or principal), the future value (or cash balance), and a type that specifies whether payments are due at the beginning or end of the period.

Syntax:

=RATE(Nper, Pmt, Pv, [Fv], [Type], [Guess])

Where:

• Nper (required): Total number of payment periods.
• Pmt (required): Payment made each period; it cannot change over the life of the annuity.
• Pv (required): Present value, or the total amount that a series of future payments is worth now.
• Fv (optional): Future value or cash balance after the last payment; if omitted, Excel assumes it’s 0.
• Type (optional): Indicates whether payments are due at the beginning (1) or end (0) of the period; if omitted, Excel assumes 0.
• Guess (optional): Initial guess for the rate; if omitted, Excel uses 10%.

 

Step-by-Step Guide to Using RATE Function

Example 1: Calculating Loan Interest Rate

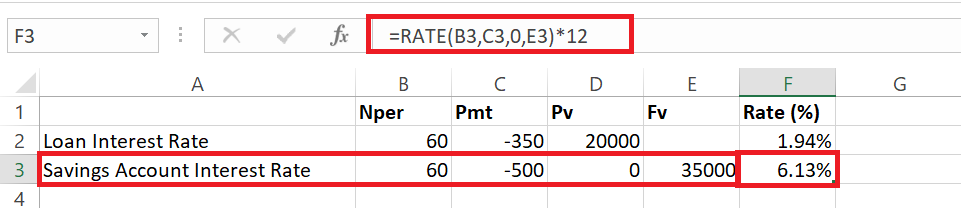
Ready to see the RATE function in action? Let’s say you’ve got a loan of $20,000 that you want to pay off in 5 years (60 months) with a monthly payment of $350. Here’s how you’d set that up:

• In cell B2, Nper (total number of payments)= 60
• In cell C2, Pmt (payment amount per period)= -350 (negative because it’s an outgoing payment)
• In cell D2, Pv (present loan amount)= 20,000

The RATE function formula you’d use in Excel looks like this:

=RATE(Nper, Pmt, Pv)*12 or “=RATE(60, -350, 20000)*12” or “=RATE(B2,C2,D2)*12”

Multiplying by 12 gives you the annual interest rate. In a few clicks, you’ll have the percentage rate that brings your financial picture into focus.

Example 2: Figuring Out Savings Account Interest Rate

Switching gears to savings—let’s determine the growth rate of your money in a savings account. Suppose you plan to save $500 monthly for 5 years, aiming for a goal of $35,000. You’d set your parameters as follows:

• In cell B3, Nper (total number of deposits): 60
• In cell C3, Pmt (monthly savings contribution): -500 (it’s negative as this is what you’re putting in)
• In cell E3, Fv (desired future value): 35,000

To find the interest rate that will get you to your savings goal with these inputs, punch in the formula: =RATE(60, -500, 0, 35000)*12 or =RATE(A3,B3,0,D3)*12 in Excel. This computation provides the annual interest rate that turns your savings plan into a success story.

 

Troubleshooting Common Issues with RATE Function

Dealing with #NUM! and #VALUE! Errors

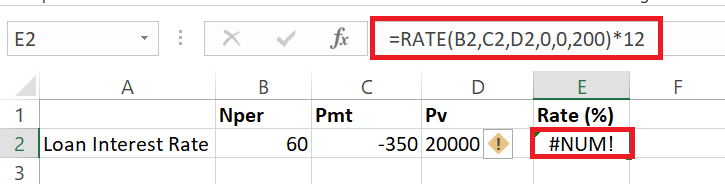
If RATE is throwing you curveballs with #NUM! or #VALUE! errors, keep calm and troubleshoot on. The #NUM! error often waves hello when RATE struggles to find a rate after 20 tries, so try a closer guess. It also appears that your inputs are a bit off in the world of finance—negative payment periods or outlandish figures, for example.

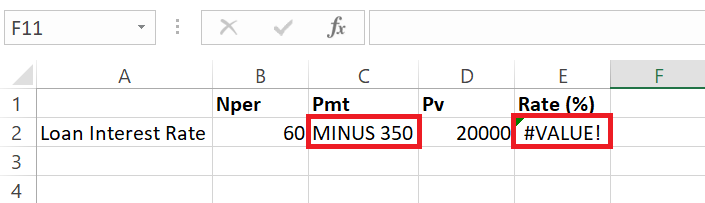
On the other hand, #VALUE! pops up if there’s a non-numeric character lurking in your inputs. Double-check for any typos or missteps and replace them with the solid, reliable numbers that RATE expects.

Adjusting Calculation Settings for Accurate Results

To nail down accuracy in your RATE calculations, some fine-tuning may be required. Make sure that the signs on your cash flows (Pmt, Pv, and Fv) are consistent with their direction – outgoing payments are negative, and incoming cash is positive.

Twiddle with the ‘Guess’ value if RATE seems stumped; it guides Excel on where to begin the search for the interest rate. And if the result looks off, like you’re getting a zero when you expected more, it might just be the cell formatting. Adjust it to show more decimal places, and voilà! Accuracy restored!

 

Advanced Applications of RATE Function

Analyzing Investment Returns with Precision

In the realm of investments, precision is not just nice to have; it’s a non-negotiable. Pivoting your decisions on the precise rate of return can make the difference between profit and loss. By employing the RATE function, you’re able to decode the exact interest rate needed for money today to grow to a desired sum tomorrow. This helps you to dissect the performance of different investment vehicles, compare those rates to market returns, and choose the one that best aligns with your risk profile and return expectations.

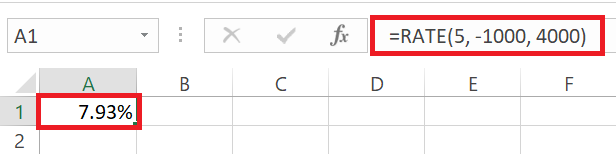
Suppose you’re considering investing in a bond that pays $1,000 annually for 5 years, with an initial investment of $4,000. To calculate the annual interest rate for this investment, you can use the RATE function: “=RATE(5, -1000, 4000)

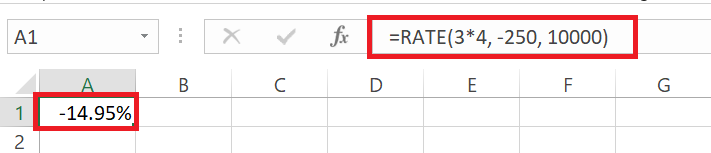
In cases where the investment generates periodic returns, such as quarterly dividends, you can adjust the RATE function accordingly. For example, if you’re investing $10,000 and receiving quarterly payments of $250 for 3 years, the formula would be: “=RATE(3*4, -250, 10000)”

 

Comparing RATE Function with Related Excel Tools

RATE Function Versus Other Financial Functions

While RATE shines bright in determining interest rates, it’s part of a family of Excel financial functions each with their own specialty. Compared to PMT for calculating payments, or PV and FV for present and future values, RATE zeros in on the rate of return or interest for a given set of cash flows.

These functions often work together like pieces of a financial puzzle – RATE might establish what interest rate you need, while PMT calculates each payment under that rate. Depending on your goal, one function may suit better, but for nailing down interest rates, RATE undoubtedly takes the crown.

When to Use RATE Function Over Alternatives

Switching to RATE from its alternatives makes perfect sense when your focus is the interest rate itself. Whether you’re calculating what rate of return you need on an investment or the interest you’ll pay on a loan, RATE steps up where other financial functions may not venture.

If your puzzle is ‘How much will my regular savings grow?’ or ‘What interest will I end up paying?’, RATE is your answer, fitting the pieces together with finesse. For a broader financial analysis, it might team up with other functions, but RATE’s expertise is unmistakably in solving interest rate queries.

 

FAQs About Excel’s RATE Function

Q.1 What is the formula for the rate?

The formula for the RATE function in Excel is =RATE (nper, pmt, pv, [fv], [type], [guess]), where ‘nper’ is the number of periods, ‘pmt’ is the payment amount per period, ‘pv’ is the present value, and ‘fv’, ‘type’, and ‘guess’ are optional arguments for future value, timing of payments, and your interest rate estimate, respectively.

Q.2 What is the RATE function in Excel, and how does it work?

The RATE function in Excel calculates the interest rate for a given period based on a series of future payments (pmt), a present value (pv), and, optionally, a future value (fv), with the type of payment timing and an initial guess for the rate. It employs trial-and-error to iteratively determine the rate that equates the present value of an investment with its future value.

Q.3 How do I handle situations where the RATE function returns an error or inaccurate results?

If the RATE function returns an error or inaccurate results, double-check the sign of your cash flows and ensure present value and future value are opposites. Verify the number of periods is correct, and format the cell to show decimal places if the result appears as zero. If you see a #NUM! error, adjust your guess or the inputs, and if it’s a #VALUE! error, ensure all values are numeric. Limit iterations for more precise outputs if needed.

Q.4 How will your investment grow in terms of cagr?

To find out how your investment will grow in terms of Compound Annual Growth Rate (CAGR), use the Excel RATE function with your total time period as ‘nper’, initial investment as ‘pv’, the final amount as ‘fv’, and payments (pmt) as 0 since it’s a one-time investment. The function will give you a periodic rate which can be annualized to reflect CAGR.

Q.5 What is the effective rate function in Excel?

The EFFECT function in Excel calculates the annual effective interest rate, given the nominal rate and the number of compounding periods per year. It translates a stated interest rate into the equivalent rate that takes compounding into account. The formula in Excel is =EFFECT(nominal_rate, npery), where ‘nominal_rate’ is the nominal interest rate, and ‘npery’ is the number of compounding periods per year.