Excel TAN Formula – Step by Step Tangent Calculations

When working with trigonometry in Excel, one of the essential functions you’ll encounter is the TAN formula. As someone who frequently uses Excel for a variety of tasks, including data analysis and calculations, I’ve found the TAN formula to be incredibly useful for calculating the tangent of an angle. Let me walk you through everything you need to know about it.

Key Takeaways:

• The TAN function calculates the tangent of an angle in radians, requiring degree-to-radian conversion using the RADIANS function if the angle is in degrees.
• Use =TAN(number) for straightforward tangent calculations, ensuring angles are in the correct format for accurate results.
• Combine TAN with logical operations like IF statements for advanced formulas and dynamic categorizations, such as slope classifications.
• Avoid common errors by ensuring inputs are numeric, angles aren’t undefined (e.g., 90° or 270°), and radians are used correctly.
• Verify accuracy by testing with known values (e.g., TAN(45°) = 1) and increasing decimal precision for more detailed calculations.

 

Grasping the Basics of the Excel TAN Formula

What Is the TAN Function in Excel?

The TAN function in Excel calculates the tangent of a given angle. The angle is specified in radians—a fundamental aspect of understanding how Excel’s trigonometric functions operate. It’s an essential function when working with geometric shapes, mathematical problems, or any scenario where angle properties are relevant.

Syntax and Parameters for TAN in Excel

In Excel, using the TAN function is straightforward. I enter the following syntax in the cell where I want to see the result: =TAN(number).

The ‘number’ parameter represents the angle in radians for which we are trying to calculate the tangent. It’s important to remember that if the angle is provided in degrees, it must be converted into radians first, typically by using the RADIANS function in Excel.

 

Tangible Examples of TAN at Work

Calculating the Angle’s Tangent With Precision

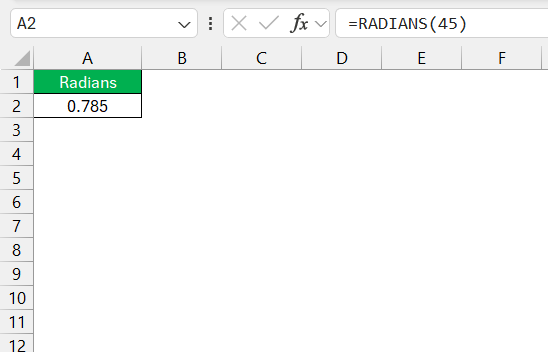
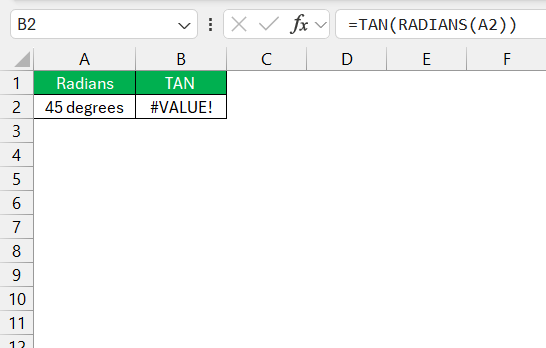
To calculate the angle’s tangent with precision, I first ensure the angle is in the correct format—radians. Let’s say I am dealing with an angle of 45 degrees. I would convert this to radians using =RADIANS(45).

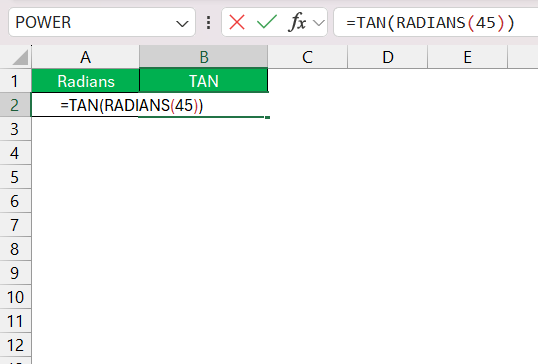
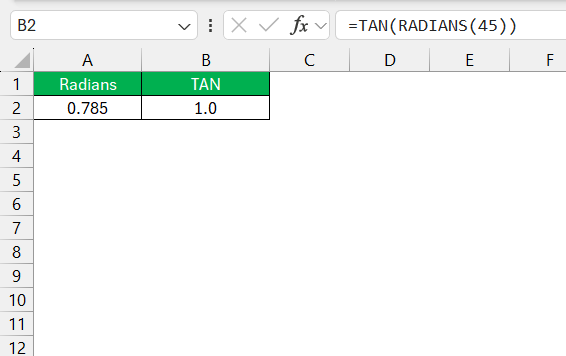
Then, I apply the TAN formula like this: =TAN(RADIANS(45)).

By hitting enter, Excel gives me the precise tangent of the angle.

This method allows for accurate and quick calculations, which are pivotal in analyses and designs where precise measurements matter significantly.

Real-World Scenarios: Heights and Distances

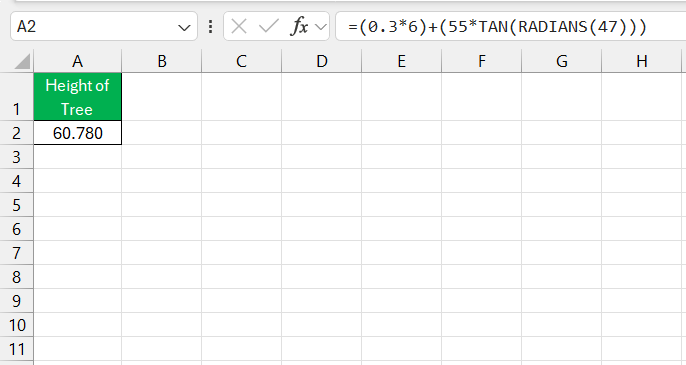
In real-world scenarios, the TAN formula can be incredibly useful. For example, imagine needing to calculate the height of a tree given the distance from the tree and the angle of elevation. With a simple measure of the angle from eye level and a known distance, we can apply the tangent to determine the height.

Let’s say a 6-foot tall person is standing 55 meters from a tree, looking up at the top at a 47-degree angle. Converting the person’s height into meters and using the TAN function, we get the height of the tree: (0.3*6)+(55*TAN(RADIANS(47))), finding it to be approximately 60.78 meters tall.

Similarly, when calculating distances, such as the horizontal distance from a point on a hill to the base, knowing the height and the angle of inclination provides enough data to utilize the TAN formula effectively. It proves to be an invaluable tool across fields such as construction, navigation, and surveying.

Including statistical data or a graphical representation can put this into perspective, such as

 

The Intersection of TAN with Other Excel Functions

Integrating Logical Operations with TAN for Advanced Formulas

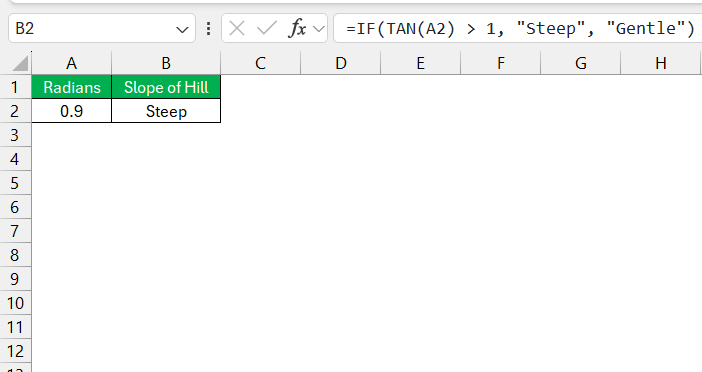
Integrating logical operations with TAN gives Excel formulas more versatility. We can manipulate data based on conditions, such as categorizing slopes of hills into ‘steep’ and ‘gentle’ categories. For example, I might employ an IF statement alongside TAN: =IF(TAN(radians) > 1, "Steep", "Gentle").

This checks the tangent value and returns ‘Steep’ if it exceeds 1, which corresponds to a 45-degree angle, a common threshold for considering a slope steep.

This advanced use of TAN with logical operations can be demonstrated in more complex scenarios, such as auto-adjusting financial models or setting up conditional formatting rules.

 

Common Errors and How to Avoid Them

While using the TAN function, you might encounter some errors. Here are the most common ones and how to address them:

• #VALUE! Error: This occurs if the input is not a numeric value. Ensure that the angle is a number or a cell reference containing a number.

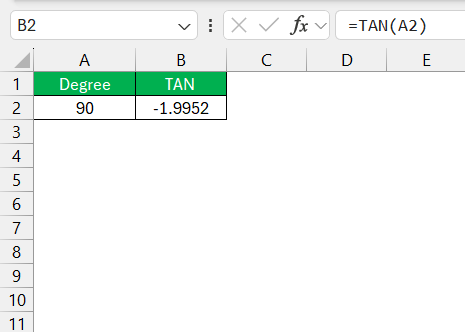
• #NUM! Error: The tangent function is undefined for angles where the cosine is zero, such as π/2 (90 degrees) or 3π/2 (270 degrees). Avoid using these values as input.
• Incorrect Units: If you input degrees directly without converting them to radians, the result will be incorrect. Always convert degrees to radians first.

 

Tips and Tricks for Working with TAN

Avoiding Common Pitfalls in Tangent Calculations

To sidestep common pitfalls in tangent calculations, I stay vigilant for a few things. I never forget to convert degrees to radians using the RADIANS function before applying TAN formula.

Moreover, understanding that TAN returns a ratio and not an angle is vital for interpreting results correctly. I also keep in mind that using a negative angle results in a negative tangent value, which is a correct outcome, but sometimes unexpected.

By staying alert to these nuances, I find that I can prevent most errors and ensure the reliability of my calculations when using TAN.

Ensuring Accuracy in Your Results

Ensuring accuracy in tangent calculations involves a couple of crucial steps. First, I verify the mode of my calculator or Excel to ensure it’s set to radians when entering angles directly. Second, I always perform a sense check on my results.

Using known values, such as the tangents of 45 degrees (1) or 0 degrees (0), allows me to confirm that the TAN formula is behaving as expected. If there’s any discrepancy, I double-check my formulas and conversions.

Additionally, precision can be increased by using more decimal points in angle measures where necessary, although Excel usually handles a significant number of decimal places by default.

 

Frequently Asked Questions

What is the tan formula?

The TAN formula in Excel calculates the tangent of an angle provided in radians. Tangent is a trigonometric ratio of the sides of a right-angled triangle that’s essential for various mathematical and engineering calculations.

How to calculate tan in Excel?

To calculate tan in Excel, enter =TAN(number) into a cell, where ‘number’ is the angle in radians. If your angle is in degrees, first convert it by using =RADIANS(degrees). Then apply the TAN function.

How Do I Calculate the Inverse of a Tangent in Excel?

Calculate the inverse of a tangent in Excel using the ATAN function. Simply type =ATAN(number) into a cell, and it will return the arctangent of your ‘number’, in radians.

Can TAN Be Used in Conjunction with Conditional Formatting?

Yes, TAN can be used with conditional formatting in Excel to dynamically apply formatting based on the tangent values of certain angles. For example, highlighting cells containing tangent values greater than 1.

What Are Some Common Errors to Look Out For When Using TAN?

When using TAN, watch for a #VALUE! error from non-numeric inputs – always ensure your angles are numbers. A #NUM! error signifies an invalid number, like a tangent of an angle that Excel can’t calculate. Also, remember to use radians not degrees, unless converted.