The Ultimate Guide to Future Value Annuity Calculator in Excel Finance

When it comes to financial planning, understanding the future value of annuities can be a game-changer. Whether you’re saving for retirement, planning for a big purchase, or simply curious about investment growth, creating a Future Value Annuity (FVA) calculator in Excel can help.

In this guide, I’ll show you how to set up a Future Value Annuity calculator step-by-step in Excel, and we’ll cover the essential formula for this calculation.

Key Takeaways:

• The future value of an annuity is crucial for financial planning, helping us predict the growth of investments.
• Annuities offer a steady income stream, ideal for retirement or large purchases.
• Excel’s FV function makes calculating future annuity values straightforward by defining the rate, periods, and payment structure.
• Annuity types (Ordinary vs. Due) impact the final value, with Annuity Due yielding slightly higher returns due to earlier payments.
• Excel’s financial functions, like PMT, RATE, and NPER, allow us to solve for various annuity-related calculations, aiding in effective financial forecasting.

 

Understanding the Future Value of an Annuity

The Basics of Annuity and Its Importance

An annuity is an investment that can provide you with a steady income stream, typically for retirement. It’s a financial product that you purchase or invest in with a lump sum or through periodic payments.

The allure of an annuity lies in its ability to produce revenue over time, which is crucial for those who want to ensure they have a secure financial footing as they age. By understanding annuities, we can make more informed decisions about our long-term financial health.

Defining Future Value in Financial Terms

Future value (FV) is a concept that tells us what an investment made today will be worth at a specified time in the future, given a certain rate of return or interest rate. This financial metric is essential in reckoning how much we might accumulate over time from savings or what the ultimate payoff of an investment might be.

It embodies the principle of the time value of money, which posits that a dollar today is worth more than a dollar tomorrow because of its potential earning capacity. When we understand the future value, we can better plan for goals like retirement or big purchases by forecasting the growth of our assets.

 

Harnessing Excel’s FV Function

Breaking Down the FV Function Syntax

The FV function in Excel is a financial function designed to calculate the future value of an investment based on periodic, constant payments and a constant interest rate. To fully harness this function, we need to comprehend its syntax:

FV(rate, nper, pmt, [pv], [type])

Here’s a breakdown:

• rate: This is the interest rate per period. To ensure accuracy, we need to match the rate with the frequency of payments—meaning if we make monthly payments, we provide a monthly interest rate.
• nper: This stands for the total number of payment periods in an annuity. For example, if we invest in a 10-year bond with semi-annual payments, nper would be 20.
• pmt: This represents the payment made in each period and must remain constant throughout the annuity.
• [pv]: It’s the present value or the total amount that a series of future payments is currently worth. If we’re starting an annuity with no initial investment, we’d skip this or set it to 0.
• [type]: This tells Excel when the payments are due—0 for end of the period (ordinary annuity) or 1 for the beginning (annuity due).

Understanding each part of the syntax is vital for effectively using the FV function to predict financial outcomes.

Applying the FV Formula for Periodic Payments

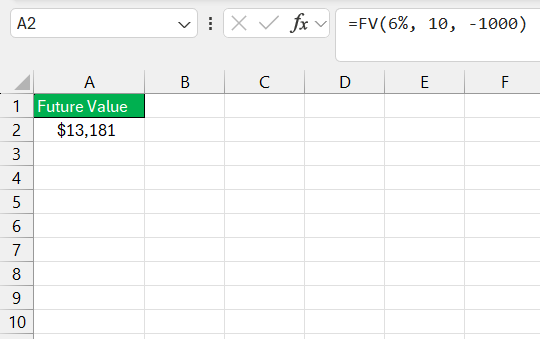
To apply the FV formula effectively for periodic payments, it’s crucial that we correctly identify and input each argument based on our annuity setup. In our hypothetical example, with yearly payments of $1,000, a 10-year term, and a 6% annual interest rate, the FV formula is executed as follows:

=FV(rate, nper, pmt)

We input the annual interest rate into ‘rate’, the number of years into ‘nper’, and since payments are money out, ‘pmt’ is input as a negative number:

=FV(6%, 10, -1000)

This calculation tells us how much we’ll have saved at the end of 10 years, considering the specified payments and interest rate. However, it’s important to ensure that the rate corresponds with the payment period. If we make monthly contributions, the rate must be divided by 12, and the periods must be multiplied by 12 accordingly.

 

Advanced Tips on Future value Annuity Calculator

Annuity Types: Ordinary Annuity vs. Annuity Due

An Ordinary Annuity involves payments made at the end of each period, such as the end of the month or the end of the year. This type of annuity is common for investments like retirement savings, where deposits are typically made after income is earned for that period.

In contrast, an Annuity Due requires payments at the beginning of each period. This structure is often used for expenses like rent, where payment is needed at the start of the month or period. The timing difference between these two types of annuities affects the total amount accumulated, with annuities due typically accumulating slightly more interest over time due to the earlier payment schedule.

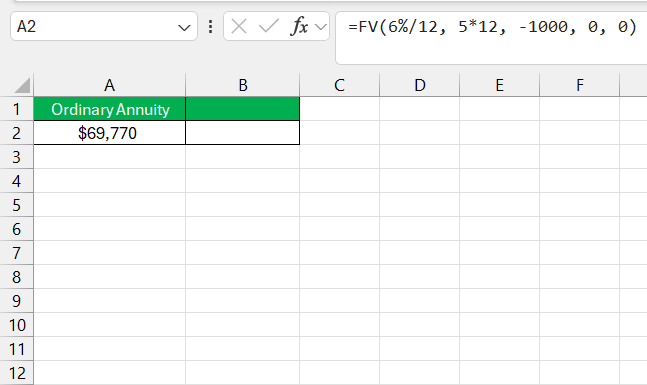
Suppose I want to save $1,000 each month for 5 years with an interest rate of 6% compounded monthly. Let’s look at how much I would have with each type of annuity.

Ordinary Annuity Calculation: =FV(6%/12, 5*12, -1000, 0, 0)

Here, the type argument is 0, which specifies that payments are made at the end of each period.

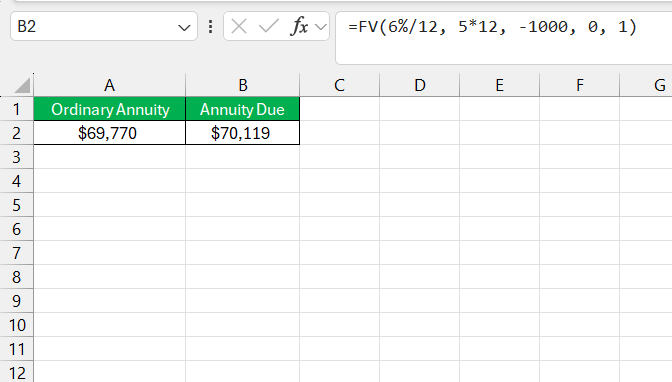
Annuity Due Calculation: =FV(6%/12, 5*12, -1000, 0, 1)

Here, the type argument is 1, indicating payments are made at the beginning of each period.

Because the Annuity Due allows each payment to earn interest for an additional period, it results in a higher future value. In this case, the Annuity Due yields around $3,339 more than the Ordinary Annuity after 5 years.

Solving for Payment Amount, Interest Rate, and Number of Periods

Solving for different variables in an annuity scenario can be a bit tricky, but Excel’s financial functions simplify this process greatly. Let me walk you through how each component can be determined:

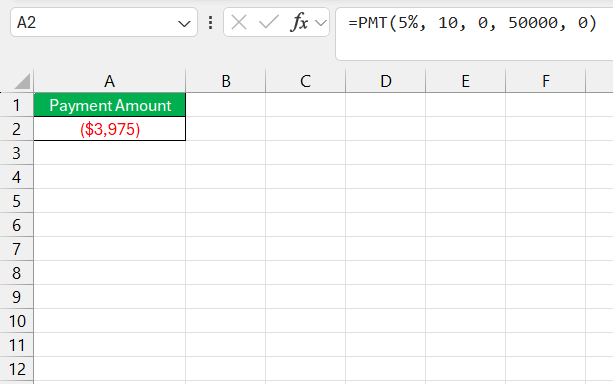
• Payment Amount (PMT): If we want to know how much to contribute to reach a target amount, we leverage the PMT function. For example, if we aim for $50,000 over 10 years at a 5% interest rate, the PMT function can calculate the annual payment.

=PMT(rate, nper, pv, fv)

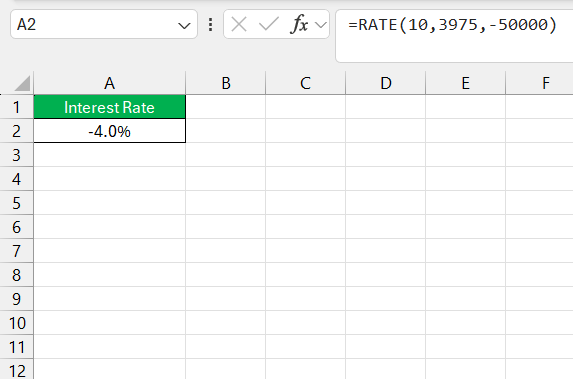
• Interest Rate (RATE): To solve for the interest rate, we use the RATE function. Given an investment’s present and future values, along with the payment and term, the RATE function can find the interest rate required to achieve the future value.

=RATE(nper, pmt, pv, fv)

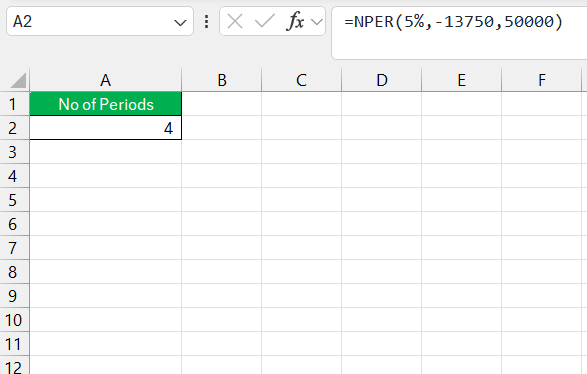
• Number of Periods (NPER): Finding out how long it will take to reach a future value is a job for the NPER function. With known payments, interest rate, present, and future value, the NPER function can reveal the number of periods needed.

=NPER(rate, pmt, pv, fv)

For any of these calculations, it’s critical to ensure all the rates and periods are consistent. Monthly rates must be accompanied by monthly periods, and vice versa for annual values.

FAQs on Annuity Calculations in Excel

How Do I Make a Future Value Calculator in Excel?

To make a Future Value calculator in Excel, set up a worksheet where you input variables like payment amount, interest rate, and number of periods. Use the FV function: =FV(rate, nper, pmt, [pv], [type]). Input your rate divided by the number of compounding periods per year into ‘rate’, the total number of compounding periods into ‘nper’, and the payment into ‘pmt’. If you have a present value or want to specify payment type, include ‘pv’ and ‘type’ in your formula. Press Enter, and Excel will display the future value for you.

Can Excel Calculate the Future Value of an Annuity with Irregular Payments?

Yes, Excel can handle calculations for the future value of an annuity with irregular payments. Use the cash flow analysis functions, such as XNPV or XIRR, which allow for differing payment amounts and intervals. Input each payment as a separate cash flow at the appropriate time to accurately determine the future value of such an investment.

What Are Some Common Mistakes When Using Excel for Future Value Calculations?

Common mistakes include not matching the rate with the payment frequency (e.g., using an annual rate with monthly payments), misaligning the payment type with the annuity type, inputting payments as positive rather than negative numbers, and not accounting for the present value when it’s necessary. Always double-check inputs for accuracy.

What’s the present value of an annuity?

The present value of an annuity is the total amount that a series of future fixed payments is worth right now. It’s calculated by discounting those future payments back to the present using a specific discount rate, which reflects the time value of money.

What’s the difference between the present value and future value?

The present value (PV) is the current worth of a future sum of money or stream of cash flows given a specified rate of return, while future value (FV) measures what this sum will grow to in the future. PV discounts the future amount to understand its value today, whereas FV calculates the growth of a present value at a specified yield or interest rate over time.