How to Calculate Natural Log in Excel with the LN Function

Excel is a powerful tool used for a variety of applications, ranging from data analysis to financial forecasting. One of its lesser-known but highly useful functions is the LN function. This function calculates the natural logarithm, a crucial concept in mathematics associated with growth processes and used extensively in finance, science, and engineering. In this article, we will learn about the LN function and its application.

Key Takeaways:

• The LN function in Excel calculates the natural logarithm of a positive number, useful for modeling exponential growth and decay.
• It differs from the LOG function by specifically using the base “e,” making it ideal for continuous growth scenarios.
• To use LN, type =LN(value) in a cell, ensuring the input is a positive number to avoid errors.
• LN can be combined with other functions like EXP, IF, or SUMPRODUCT for advanced analysis and better forecasting.
• It is widely used in finance, science, engineering, and data analysis to simplify complex exponential relationships.

 

What is the LN Function in Excel?

Basic Definition and Purpose

The LN function in Excel is designed to compute the natural logarithm of a given number. A natural logarithm is the logarithm to the base of the mathematical constant “e,” approximately equal to 2.71828. The primary purpose of this function is to simplify calculations related to exponential growth and decay processes.

It transforms multiplicative relationships into additive ones, which are easier to analyze and interpret. By using the LN function, users can effectively model natural growth processes found in fields like microbiology and finance.

How It Works Compared to Other Logarithmic Functions

The LN function specializes in calculating logarithms with the base “e,” contrasting with the LOG function in Excel, which can handle any user-specified base. While both functions serve to reveal the power to which a base must be raised to achieve a given number, their applications diverge based on their bases.

The LN function is optimal for natural and exponential growth scenarios, commonly seen in continuous compounding and natural processes. Conversely, the LOG function, with its flexibility to adjust bases, is more versatile for computations involving standard logarithmic scales like base 10 or base 2, making it suitable for a broader range of mathematical and engineering tasks.

 

Step-by-Step Guide to Using the LN Function

Entering the LN Formula in Excel

To input the LN formula in Excel, follow these straightforward steps for accurate and efficient calculations. First, click on the cell where you want the result to appear.

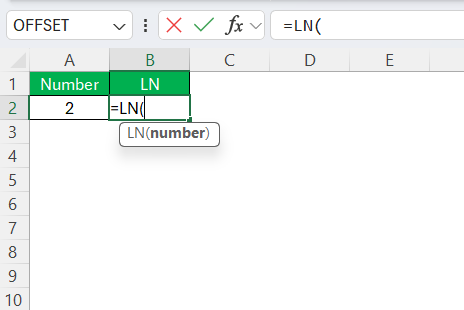
Type =LN( to initiate the function, and observe how Excel provides a handy tooltip displaying the necessary syntax.

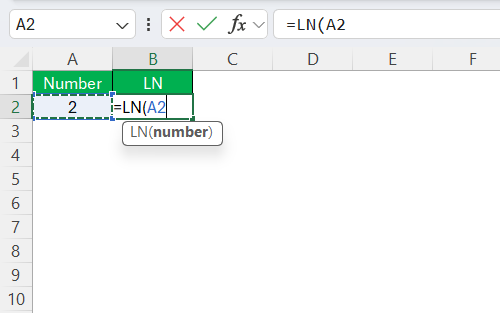
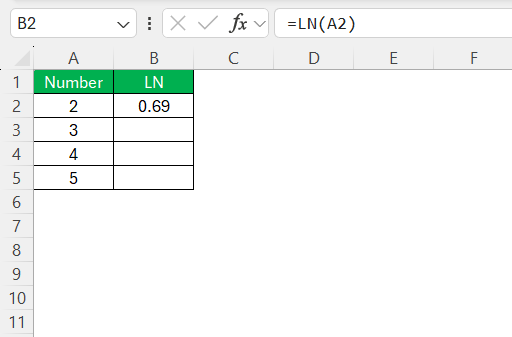
Enter the number or cell reference for which you seek the natural logarithm. For example, if the value resides in cell A2, you would type =LN(A2).

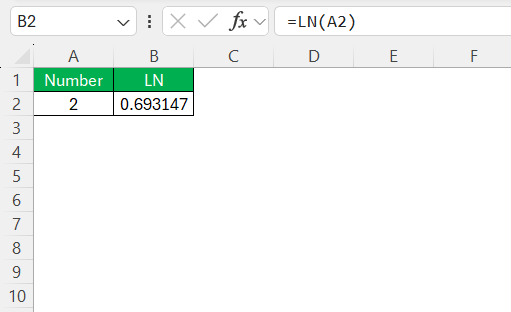
Finally, close the parenthesis and press Enter.

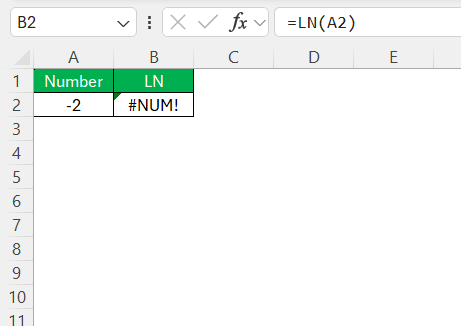
The cell will now display the natural logarithm of your specified number. Excel only processes positive numbers with the LN function, so ensure your input is valid to avoid errors.

Common Parameters and Arguments

When employing the LN function in Excel, it’s important to correctly understand its parameters and arguments to ensure accurate outcomes. The primary argument for the LN function is a positive real number, which can be a direct numeric value, a reference to a cell containing the number, or a formula that results in a positive number.

For example, in the expression =LN(5) or =LN(B2), “5” and “B2” are the arguments representing the value for which the natural logarithm is calculated. It’s crucial to remember that the LN function cannot process negative numbers or zero, as these inputs will result in errors. Double-check that your numbers are positive before applying the LN function for smooth calculations.

 

Tips for Accurate Calculations

To ensure accuracy when using the LN function in Excel, consider the following tips:

• Verify Input Values: Always check that your input values are positive numbers. Negative values or zero will cause the LN function to return errors, disrupting your calculations.

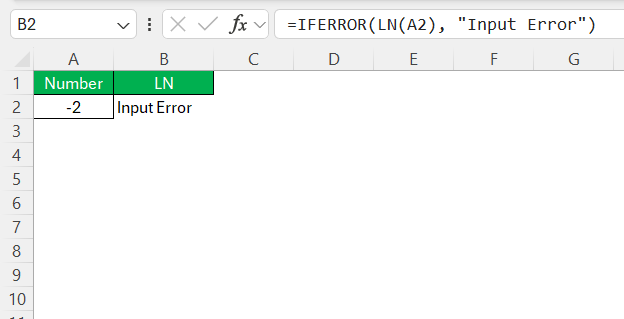
• Use IFERROR for Error Handling: Wrap your LN function in an IFERROR statement, such as =IFERROR(LN(A2), "Input Error"). This way, you replace error messages with a more informative notice, prompting you to check the input.

• Absolute Cell References: When copying the LN formula across cells, decide if you need relative or absolute cell references. Use dollar signs, like =LN($A$1), to fix the reference if needed.
• Double-Check Formulas: Before finalizing, thoroughly inspect the formulas to ensure all component parts and cell references are correct. A minor oversight in references can lead to substantial discrepancies in results.
• Experiment and Learn: The more you use and experiment with the LN function, the better you’ll understand its capabilities and nuances. Don’t hesitate to try it in combination with other Excel functions.

By following these tips, you’ll enhance the precision and reliability of your logarithmic calculations.

 

Advanced Techniques and Use Cases

Combining LN with Other Functions

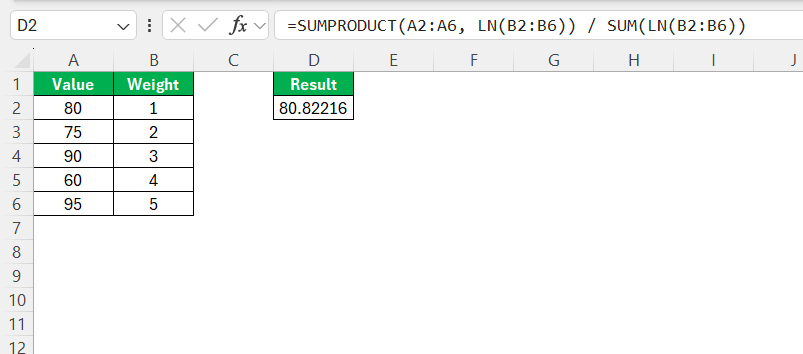
The true power of the LN function emerges when it’s combined with other Excel functions, unlocking a richer set of analytical tools. One common combination is with the EXP function to model exponential growth or decay, where LN can help solve for the exponent in equations involving exponential relationships. You might also pair LN with SUMPRODUCT for calculating weighted averages in datasets that grow exponentially over time.

For more advanced applications, consider using LN within linear regression models. By transforming the data with LN, you can linearize exponential trends, enabling better regression outputs and forecasting accuracy. Additionally, integrating LN with conditional functions like IF can create dynamic formulas that apply logarithms only under certain conditions, further enhancing flexibility in data analysis.

These combinations not only enhance the versatility and comprehensiveness of your analyses but also optimize the decision-making process, providing deeper insights into complex datasets.

Utilizing AutoFill for Trend Analysis

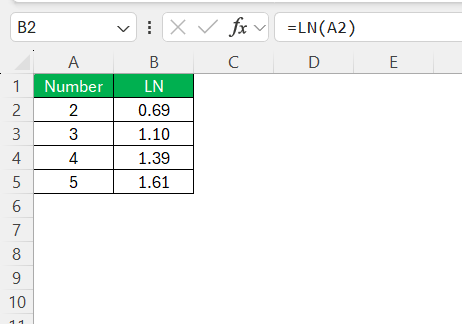
AutoFill is a powerful Excel feature that can significantly streamline the process of conducting trend analysis, particularly when using the LN function for examining exponential growth or decay. To begin, insert the LN formula in the first cell of your data range where the trend analysis is to be conducted. For example, if your series starts in cell B2, calculate the natural logarithm with =LN(A2), assuming the relevant data point resides in cell A2.

Once you have the formula in place, use the small fill handle—a solid square located at the lower-right corner of the selected cell—to drag the formula down through adjacent cells where you wish to apply the LN function. Excel automatically adjusts the row references for each new cell, ensuring that the natural logarithm is calculated for each data point in the series.

This method not only speeds up the application of the LN function across large datasets but also minimizes the chance for manual errors. By employing AutoFill, you can quickly generate a transformed dataset where the exponential trends become more linear and conducive to further analysis, enhancing the efficiency of your analytical process.

Practical Uses of the LN Function

Financial Analysis with LN

In financial analysis, the LN function proves invaluable for assessing exponential growth and examining returns on investments. For instance, when comparing logarithmic returns, analysts often prefer using LN over simple returns due to its ability to stabilize the variance, offering a more precise reflection of the underlying financial performance.

One common application is in calculating continuous compounding interest, where the LN function helps determine the growth of an investment over time through formulas like the continuously compounded interest rate. This function thus enables a more refined and accurate forecast of financial outcomes, crucial for strategic decision-making in finance.

Scientific and Engineering Applications

In scientific and engineering fields, the LN function is employed to model a variety of natural phenomena and solve complex equations. For example, it is frequently used in exponential decay models, such as radioactive decay or the cooling of an object, where processes occur at rates proportional to the current value.

Engineers often utilize the LN function to convert multiplicative processes, like those found in signal processing or material stress analysis, into additive ones, facilitating easier calculation and interpretation. Additionally, it helps in calibrating measurement scales, such as the decibel scale for sound, where logarithms convert multiplicative relationships into manageable linear scales.

Data Analysis Scenarios

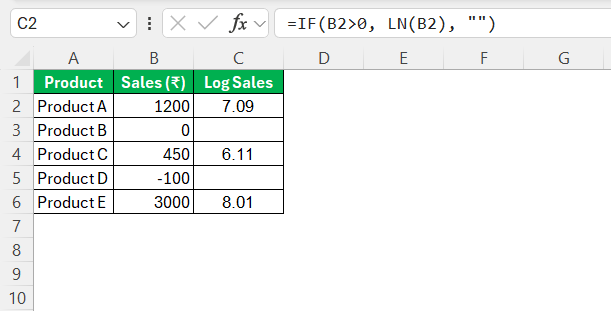
The LN function plays a pivotal role in data analysis, particularly when assessing growth trends or transformation patterns within large datasets. Analysts often use it to stabilize variance in datasets that exhibit exponential growth, thus making trends more apparent. For instance, when dealing with time series data, applying the LN function can linearize exponential trends, allowing for improved modeling and forecasting.

Furthermore, in regression analysis, the function helps transform variables, enabling the identification of relationships that might not be visible with untransformed data. These analytical benefits make the LN function a cornerstone tool for statisticians and data scientists striving for clarity in complex data scenarios.

Real-Life Business Examples

Real-world business applications of the LN function are abundant, particularly in finance, marketing, and operational strategy. For instance, companies often use the LN function to calculate the growth rate of sales revenue or the depreciation of assets over time, offering a clearer picture of a business’s financial trajectory.

In marketing, the function aids in modeling customer growth and predicting future trends based on historical data. Additionally, in logistics, businesses utilize the LN function to optimize supply chain operations by modeling time and cost variations. These examples underscore how the LN function facilitates strategic decision-making by providing deep insights into complex, dynamic business environments.

 

FAQs

What is the natural logarithm function used for?

The natural logarithm function is used for calculations involving continuous growth or decay, such as modelling exponential growth in populations, computing continuously compounded interest, and transforming data in statistical analysis for linearization and variability stabilization. It is an essential tool for simplifying complex relationships into more manageable forms.

How do you input the LN function in Excel correctly?

To input the LN function in Excel correctly, click on the cell where you want the result to appear, type =LN(, and enter a positive number or cell reference within the parentheses. Close the parentheses and hit Enter. Ensure the value or reference is positive to avoid errors.

Can the LN function handle negative numbers?

No, the LN function cannot handle negative numbers. If you input a negative number, Excel will return an error because the natural logarithm is only defined for positive numbers.

Why does the LN function return errors sometimes?

The LN function returns errors if the input is zero, negative, or non-numeric, as it is only defined for positive numbers. Double-check your inputs to ensure they are valid and meet these criteria to prevent such errors.

How do LN and exponential functions relate?

The LN and exponential functions are inverses of each other. While LN calculates the power needed for the base “e” to reach a certain number, the EXP function raises “e” to the power specified, effectively reversing the LN’s calculation. This inverse relationship allows for seamless conversion between multiplication and addition in growth models.