How to Calculate Interquartile Range in Excel Fast

Unveiling the mystery of Microsoft Excel‘s Interquartile Range (IQR) shines a light on its pivotal role in data analysis. This measure, defining the middle fifty percent of a dataset, serves as a critical gauge for understanding data dispersion. Excel emerges as a statistical ally, empowering users with tools to swiftly calculate IQR, thereby distinguishing the typical from the exceptional within datasets.

Key Takeaways:

• IQR demarcates the core spread of data, filtering out extremes to spotlight the “normal” range, which is invaluable for identifying outliers and understanding data variability.
• Leveraging Excel for statistical analysis, including IQR calculations, transforms complex data explorations into manageable tasks, making it indispensable for various professional and academic applications.
• Utilizing functions like QUARTILE and QUARTILE.INC, Excel simplifies the process of determining quartiles, thereby facilitating the efficient computation of IQR with a few straightforward steps.
• Excel’s VBA scripting enhances flexibility in statistical calculations, offering custom solutions like prompting users for data range selections to compute IQR, further tailoring the analytical process.

 

Unveiling the Mystery of Excel’s Interquartile Range

Understanding IQR in Data Analysis

Interquartile Range, or IQR, is a statistical hero in the realm of data analysis. It’s the measure of the middle fifty percent of your numbers, a compass that points out how spread out your data is. Think of IQR as the boundary between the “average” and the “outliers.” It can set the scene for understanding what’s normal and what’s exceptional in your dataset.

The Role of Excel in Statistical Calculations

Microsoft Excel isn’t just a spreadsheet software; it’s a statistical sidekick. Excel provides a versatile platform where you can perform complex statistical analyses like IQR quickly. It’s like having a digital assistant at your command, ready to crunch numbers, spot trends, and even flag potential anomalies in your data.

Excel’s functions and tools are designed to handle large datasets and automate calculations, freeing you to focus on the insights rather than the process. Whether for business forecasting, academic research, or market analysis, Excel is the go-to tool for informed data decisions.

 

Step-by-Step Guide to Calculate IQR in Excel

Using the QUARTILE and QUARTILE.INC Functions

Diving into Excel’s statistical functions, the QUARTILE and QUARTILE.INC are the magic spells for calculating quartiles. QUARTILE has been part of Excel’s toolkit for a while but is now replaced by QUARTILE.INC in newer versions. The “.INC” stands for “inclusive,” denoting that the function includes every part of your data set, from the smallest to the largest values, when determining quartile boundaries.

Here’s a simple guide on how to use the QUARTILE.INC function for IQR calculation:

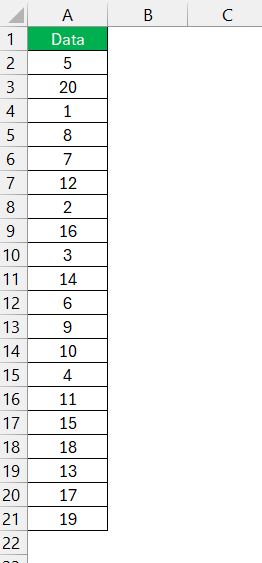
STEP 1: Open your Excel worksheet and identify the dataset range.

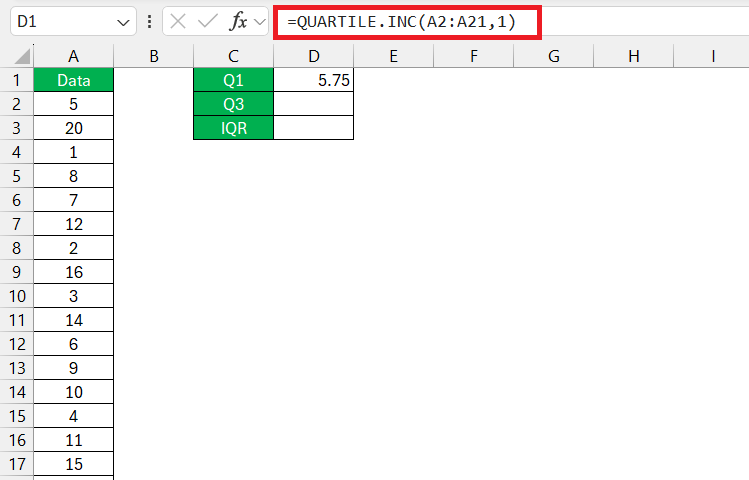
STEP 2: Select the cell where you want the IQR to appear. For Q1, enter =QUARTILE.INC(A2:A21,1).

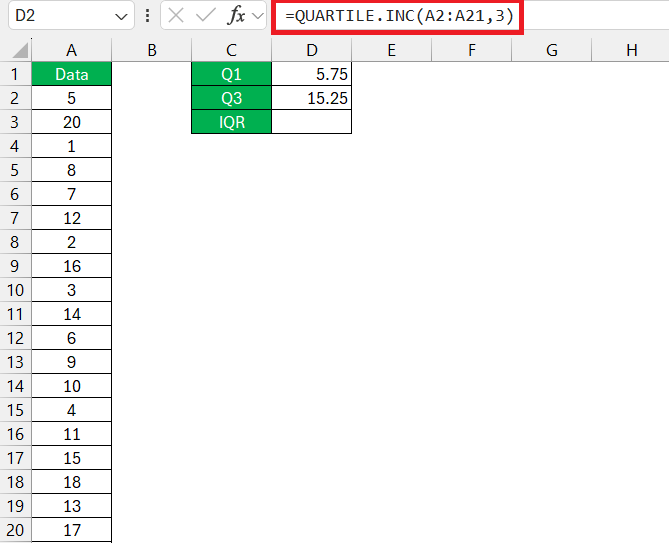
STEP 3: For Q3, enter =QUARTILE.INC(A2:A21,3).

STEP 4: To find the IQR, subtract the Q1 value from the Q3 value. Like this: D2-D1. Press Enter and voilà, your IQR is calculated!

And there you have it, you can now measure the statistical spread of your data in seconds.

 

VBA Code to Simplify Your IQR Quest

To calculate the Interquartile Range (IQR) in Excel using VBA and prompt the user to select the range, you can use the following VBA code. This code first asks the user to select a range of data. Then, it calculates the IQR by subtracting the 1st quartile (25th percentile) from the 3rd quartile (75th percentile) of the selected data. The result is displayed in a VBA message box.

Follow the steps below to calculate IQR in Excel using VBA –

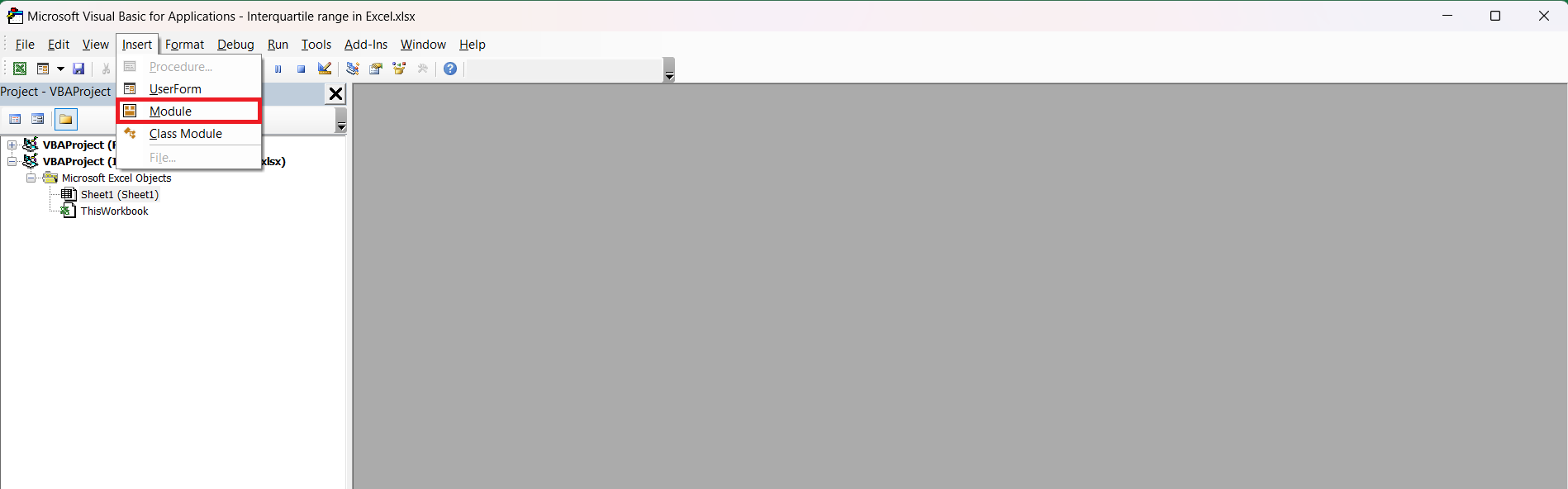
STEP 1: Press Alt + F11 to open the VBA Editor in Excel.

STEP 2: Go to Insert > Module to create a new module.

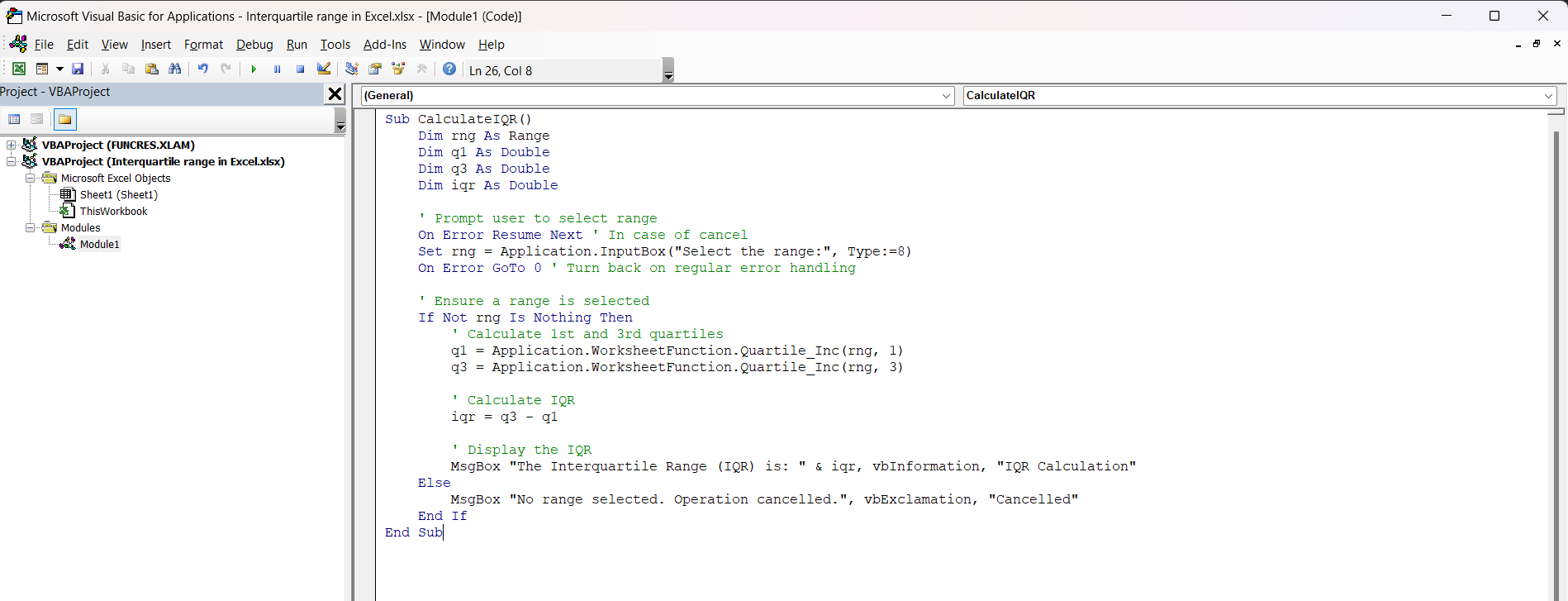
STEP 3: Copy and paste the following code into the module window.

Sub CalculateIQR()
Dim rng As Range
Dim q1 As Double
Dim q3 As Double
Dim iqr As Double
' Prompt user to select range
On Error Resume Next ' In case of cancel
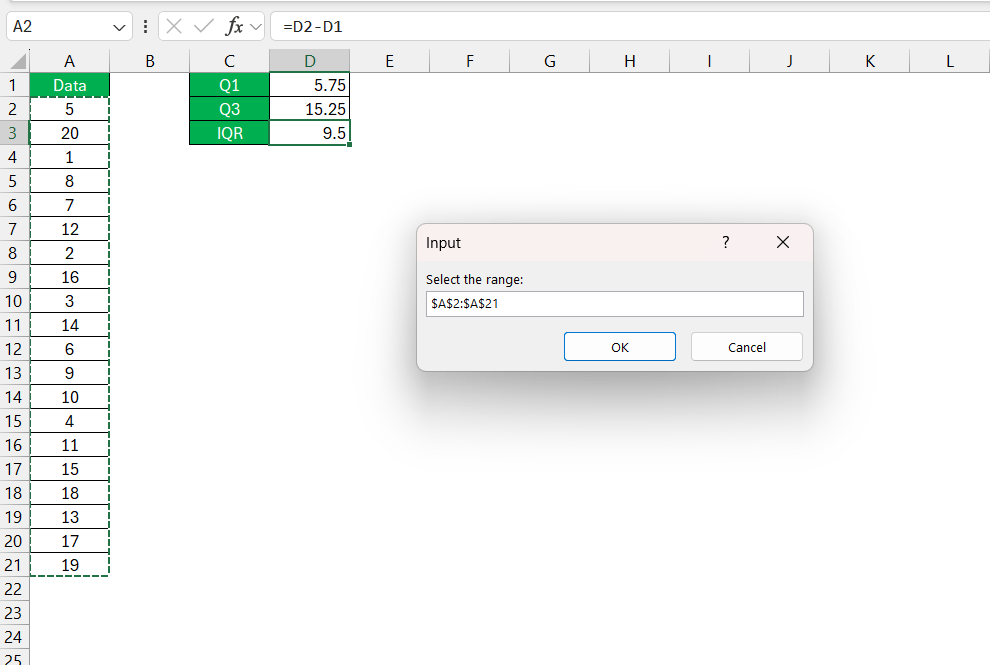
Set rng = Application.InputBox("Select the range:", Type:=8)
On Error GoTo 0 ' Turn back on regular error handling
' Ensure a range is selected
If Not rng Is Nothing Then
' Calculate 1st and 3rd quartiles
q1 = Application.WorksheetFunction.Quartile_Inc(rng, 1)
q3 = Application.WorksheetFunction.Quartile_Inc(rng, 3)
' Calculate IQR
iqr = q3 - q1
' Display the IQR
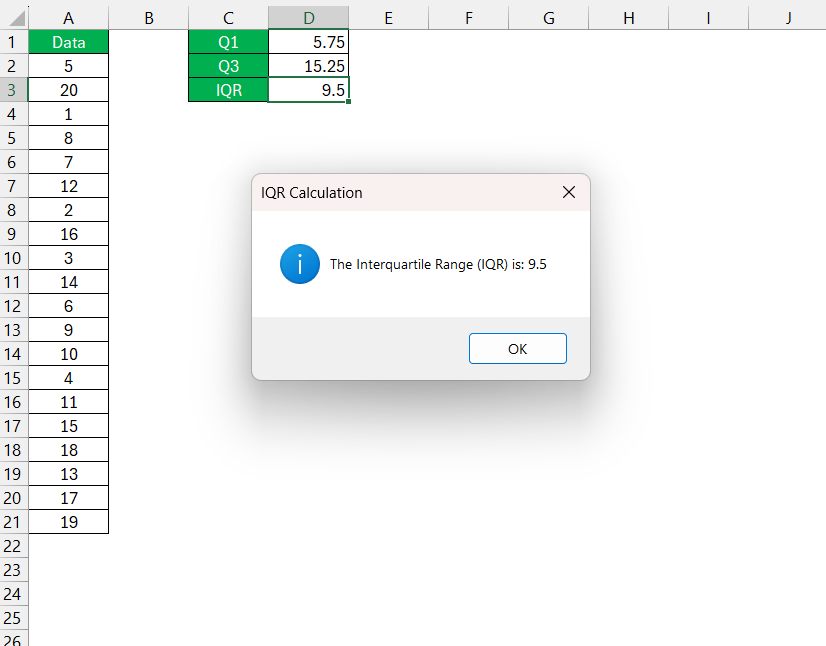
MsgBox "The Interquartile Range (IQR) is: " & iqr, vbInformation, "IQR Calculation"
Else
MsgBox "No range selected. Operation cancelled.", vbExclamation, "Cancelled"
End If
End Sub

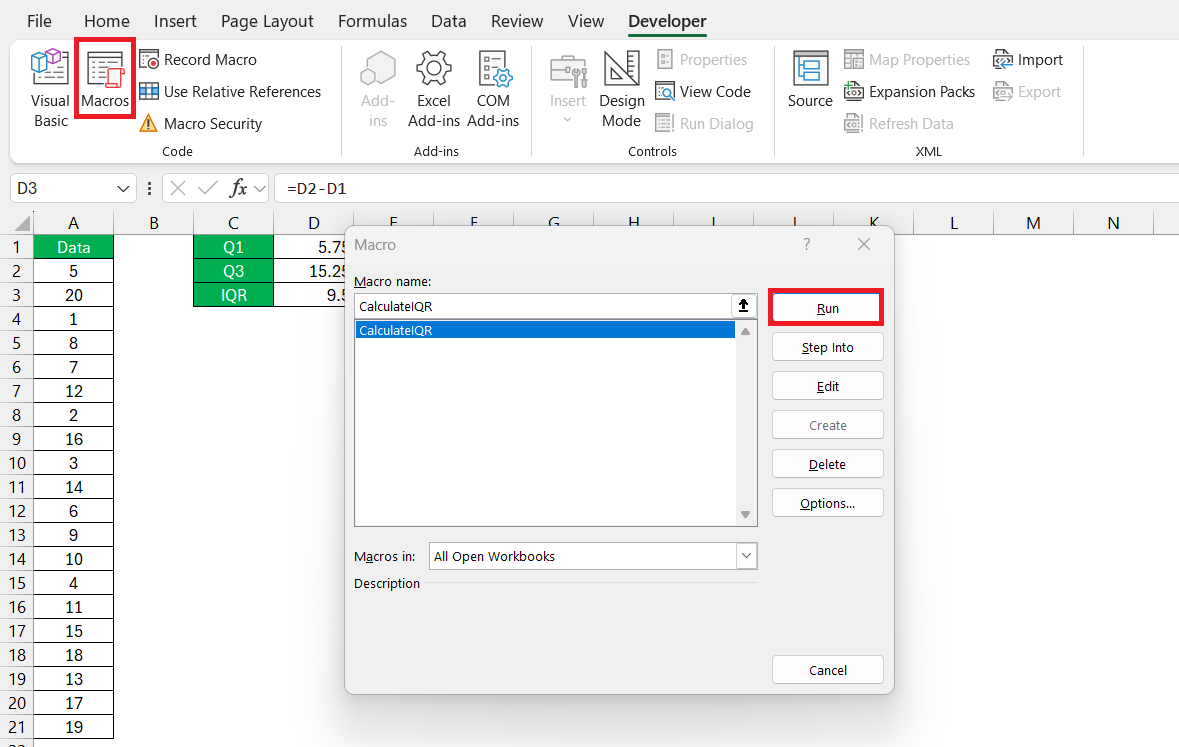
STEP 4: Go to Developer > Macros. Select the macro and press Run to execute the code.

STEP 5: Select the range containing the values.

The IQR result will be displayed in the message box.

 

Excel Tips for Quick IQR Results

Keyboard Tricks and Formula Copy Techniques

Quick and efficient—that’s how you want to tackle Excel. Keyboard shortcuts and formula copy techniques are your quiet allies. Start with the trusty Ctrl+C and Ctrl+V for copy-pasting. But it’s the lesser-known heroes you want to befriend. For instance, the Ctrl+Shift+Arrow key highlights data to the end of a range.

And don’t forget Ctrl+R and Ctrl+D, which fill the cell to the right and the cell below with the selected cell’s content, respectively.

When using formulas like IQR, these shortcuts cut steps and save time. If you have calculated Q1 and Q3, simply select both cells, use the corner square (fill handle), and drag it across to replicate the calculation for multiple data sets.

 

Ensuring Accuracy in Your IQR Computations

Accuracy in IQR computations is paramount, as it directly affects your understanding of the data’s variability. To ensure accuracy:

1. Review Your Data: Before calculating, look over your dataset for outliers or errors that could skew the IQR.
2. Use the Right Tools: Apply the correct Excel function or script and confirm that the formula references the appropriate dataset range.
3. Double-Check Results: Always check your calculated IQR against expected results or benchmarks to ensure it’s reasonable.
4. Understand the Context: Knowing how your data was collected and what it represents can alert you to anomalies in IQR calculations.
5. Consistent Conventions: Stick to the same method of determining quartiles—whether inclusive or exclusive—to maintain consistency in repeated analyses.

Taking these steps promotes the integrity of your analysis, providing you with reliable insights to guide your decisions.

 

Real-World Applications of Excel IQR

How Businesses Use IQR for Decision Making

Businesses harness the insight of IQR to make informed decisions that are data-driven. With IQR providing a glimpse into the spread of a particular dataset, companies can identify typical customer behavior and spot anomalies. It’s instrumental in fields like finance for detecting stock volatility or in e-commerce for understanding purchase amount variability.

For example:

• A retailer analyzes sales data and uses the IQR to find the regular price range of items sold, helping them to spot unusual sales activity or adjust pricing strategies.
• Human resources departments gauge salary ranges, promotions, and employee performance, identifying outliers and determining norms.

Businesses leaning on IQR have an edge; they’re more adept at navigating through data noise and grasping the essence of market trends or operational efficiencies.

IQR in Scientific Research: Making Sense of Data Variability

In scientific research, IQR is a cornerstone of exploratory data analysis. It shines a light on data variability without being overly swayed by outliers. Researchers use IQR to compare groups under different conditions or to understand the spread of control data.

For instance:

• In medicine, IQR can help to understand the range of normal blood pressure readings in a study group, discounting extreme values.
• In environmental studies, researchers might use IQR to assess the consistency of pollutant levels in various samples.

IQR’s ability to provide a more detailed picture of the data’s central tendency makes it indispensable for discovering reliable patterns and drawing valid conclusions in science.

 

Beyond IQR: Other Vital Excel Functions for Statisticians

While IQR is a striking statistical tool, Excel’s arsenal is packed with other functions that statisticians find indispensable. Among them:

1. AVERAGE and MEDIAN: to pinpoint the central tendency of your data.
2. STDEV.P and STDEV.S: for gauging standard deviation and understanding the spread around the mean.
3. CORREL: to assess the relationship and degree of correlation between two variables.
4. LINEST: for running linear regression analyses and predicting trends.
5. T.TEST: to conduct hypothesis testing and determine if differences between two datasets are statistically significant.

By mastering these functions, you can elevate your statistical analysis, uncover deeper insights, and make your Excel data work even harder for you.

 

FAQ on Excel IQR Calculation

What are Quartiles and Why is IQR Important?

Quartiles are values that divide your dataset into four equal parts, and IQR, the range between the first (Q1) and third (Q3) quartile, is vital because it shows the extent of the middle fifty percent of your data. It’s important because it provides a clearer picture of data distribution, ignoring outliers and focusing on the central chunk of data, which can be more representative of a “normal” experience.

How Do You Interpret IQR Results in Excel?

Interpreting IQR in Excel is straightforward: a smaller IQR suggests that your data points are closer together, indicating consistency, while a larger IQR points to greater spread, implying variability. In practical terms, it helps to determine the concentration and dispersion around the dataset’s median value. Using the IQR, you can identify outliers and understand the overall distribution pattern within your data.

What is Q1 and Q3 in Excel?

In Excel, Q1 and Q3 represent the first and third quartiles of your data set, respectively. Q1 is the median of the lower half of your data, meaning 25% of the data points are below it, and 75% are above. Q3 is the median of the upper half, where 75% of the data points lie below it and 25% above. These quartiles are crucial for calculating the IQR and understanding the spread of your data.

What is the formula for the interquartile range?

The formula for the interquartile range (IQR) is simple: IQR = Q3 – Q1. In this formula, Q3 represents the third quartile and Q1 represents the first quartile of your data. The result reflects the spread of the middle 50% of your values, providing a robust measure of variability that is not influenced by outliers.

Where does the term interquartile range come from?

The term “interquartile range” originates from descriptive statistics and encapsulates the range between the “inter” (or between) “quartiles” (Q1 and Q3) of a dataset. This statistical measure was developed in the 19th century to provide a robust view of the central spread of values in a data set, excluding the influence of outliers or extreme values. The IQR focuses on the middle fifty percent of data points, offering a clear view of a dataset’s variability.