How to Use LINEST Function Excel – Step by Step Guide

When I first discovered the LINEST function in Excel, I quickly realized how powerful it is for statistical analysis, especially when it comes to linear regression. If you’re like me and often need to analyze relationships between variables or predict future values, this function will become one of your go-to tools. Let me walk you through the basics of the LINEST function, its syntax, and how you can use it effectively in your work.

Key Takeaways:

• The LINEST function in Excel is powerful for performing linear regression analysis and predicting future values.
• It calculates the best-fit line and provides detailed regression statistics like slope, intercept, and R-squared.
• Using LINEST involves understanding its syntax, including optional parameters for more precise control.
• Interpreting LINEST results requires careful analysis of the outputs to ensure accuracy and reliability.
• Troubleshooting common issues with LINEST often involves checking data alignment, cleaning data, and verifying function inputs.

 

Introduction to LINEST Function in Excel

What is the LINEST Function?

The LINEST function in Excel is used to calculate the statistics for a straight line that best fits a set of given data points using the least squares method. This function returns an array of values that describe the linear trend, such as the slope, intercept, and other statistics related to the regression.

Syntax of the LINEST Function

The syntax of the LINEST function is as follows:

=LINEST(known_y’s, [known_x’s], [const], [stats])

• known_y’s: This is a required argument that represents the dependent data (y-values) you want to analyze.
• known_x’s: This is an optional argument representing the independent data (x-values). If omitted, Excel assumes x-values as {1, 2, 3, …}.
• const: This is an optional logical value (TRUE or FALSE). If TRUE or omitted, Excel calculates the y-intercept (b) normally. If FALSE, Excel forces the y-intercept to be zero.
• stats: This is an optional logical value (TRUE or FALSE). If TRUE, LINEST returns additional regression statistics. If FALSE or omitted, it only returns the slope and intercept.

 

Harnessing the Power of LINEST

Understanding the Basics: What Does LINEST Do?

At its essence, the LINEST function calculates the statistics for a line—one that best fits a dataset—using the ‘least squares’ method. This method minimizes the sum of the squares of the differences between observed and calculated values, offering a line of best fit. Essentially, LINEST determines the linear equation that describes how your dependent variable changes with your independent variable(s).

But LINEST doesn’t stop there—it also provides additional regression statistics, such as the R-squared value, standard error, and F-statistic. All these help us gauge the accuracy and reliability of the predicted trend. I like to think of LINEST as a sophisticated tool that not only draws the line but also gives you a magnifying glass to examine the fineness of that line.

Behind the Scenes: How LINEST Calculates Regression

Diving deeper behind the scenes, LINEST harnesses the power of the least squares method to perform its calculations. This involves finding the linear equation that minimizes the sum of the squares of the vertical distances of the points from the line—essentially, it’s looking for the best possible fit through your data points.

LINEST uses your data points to assemble a system of equations. It then solves these equations to determine the slope and y-intercept of the line of best fit. These coefficients are crucial—they tell you the rate at which your dependent variable is expected to change for a given change in your independent variable(s). It’s quite meticulous work, but LINEST does it swiftly, helping you leap from raw data to actionable insights in a flash.

 

Steps to Mastering LINEST in Excel

How I Use the LINEST Function

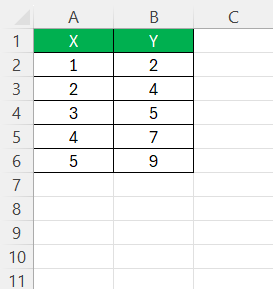
Let me share an example to show how I typically use the LINEST function. Suppose I have the following data:

To perform a linear regression on this data, I’d enter the following formula:

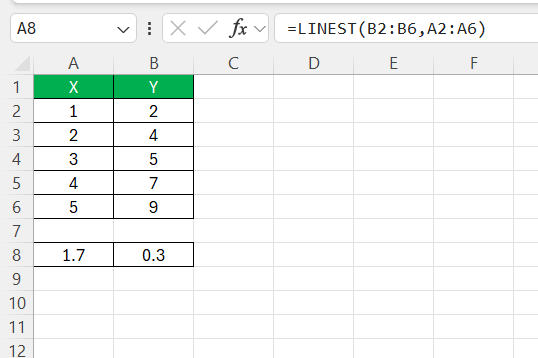
=LINEST(B2:B6, A2:A6)

This formula gives me the slope and intercept of the best-fit line. If I need more detailed statistics, I’ll use:

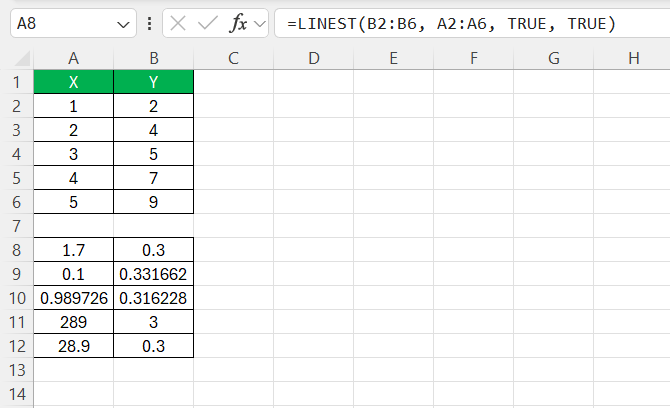
=LINEST(B2:B6, A2:A6, TRUE, TRUE)

After entering this as an array formula (by pressing Ctrl+Shift+Enter), Excel returns an array with all the extra stats I might need, such as:

• Slope
• Intercept
• R-squared value (which shows how well the line explains the data)
• Standard error (for both the slope and intercept)

Breaking Down the Output

When I use LINEST with stats set to TRUE, it returns an array filled with different statistical values. Here’s what I get:

• Slope(s): This tells me how much the dependent variable (y) changes for every unit of the independent variable (x).
• Intercept: This is the value of y when x equals zero, and it helps me understand the baseline of the data.
• R-squared value: A key metric I use to determine how well the line fits the data—higher is generally better.
• Standard errors: These give me an idea of how accurate the slope and intercept estimates are.

 

Some Practical Examples

Example 1: Simple Linear Regression

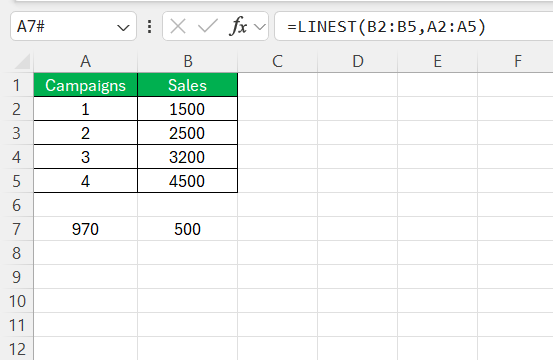
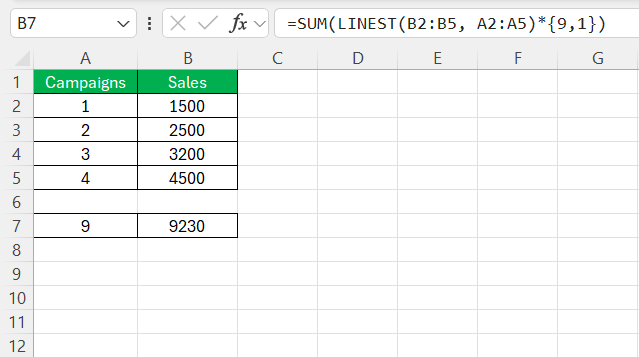
Let’s say I want to predict future sales based on the number of marketing campaigns. To find the relationship between campaigns and sales, I’d use:

=LINEST(B2:B5, A2:A5)

To predict future sales when the number of marketing campaigns is 9, we can use the following formula:

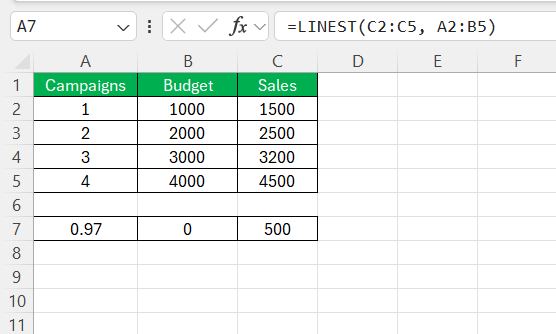
Example 2: Multiple Regression

Now, if I want to predict sales based on both the number of campaigns and the budget spent, my data might look like this.

To analyze this data, I would turn to the LINEST function with multiple independent variables:

=LINEST(C2:C5, A2:B5)

 

Things I Keep in Mind

• Array Formulas: Since LINEST is an array function, I always press Ctrl+Shift+Enter after typing the formula to ensure it calculates correctly.
• Interpreting R-Squared: I always look at the R-squared value to gauge how well the data fits, but I also consider other statistical measures to get a complete picture.

 

Troubleshooting Common Issues with LINEST

Incorrect Results: What Went Wrong?

When LINEST doesn’t behave as expected, leading to incorrect results, it’s essential to troubleshoot methodically. Common missteps often boil down to mishandled data or syntax errors. For instance, ensuring that the range of known_y's aligns correctly with known_x's is crucial, much like ensuring puzzle pieces match.

Misalignment, data gaps, non-numeric data disguised as numbers, or simply overlooking the true dynamics in the dataset can lead to skewed or incorrect outputs. These are akin to missing ingredients or incorrect quantities in a recipe; they could lead you to a result, but just not the one you hoped for.

Another aspect could be the misuse of options. For example, setting the const parameter incorrectly could inadvertently fix the y-intercept to zero when allowing it to float, which would provide a more accurate model.

Tips for Ensuring Accurate LINEST Outputs

To ensure that your LINEST outputs are as precise as a Swiss watch, consider these tips as your toolkit for success. First and foremost, verify your data layout. Structuring your data correctly is key; it should be as organized as a library, with each variable in its rightful place.

Conduct a thorough data cleaning process to remove anomalies or outliers that could distort your analysis, akin to polishing a lens for the clearest view. Opt for a visual inspection of your data with a scatter plot to confirm that a linear model is appropriate—a clear pattern should be visible, suggesting a linear relationship.

Also, pay meticulous attention to your LINEST function’s input parameters. Understanding what each parameter does, and entering them correctly is essential. It’s like dialing the combination to a safe; everything needs to be just right.

Lastly, check your results for sanity. If the outputs defy logic or your understanding of the data, don’t hesitate to double-check. Sometimes revisiting your dataset with a fresh set of eyes or seeking a second opinion might uncover overlooked errors.

 

Frequently Asked Questions (FAQs)

What is the linest function?

The LINEST function is part of Excel’s suite of statistical tools and is used for linear regression analysis. It calculates the statistics for a line by using the least squares method to find the line that best fits your data, returning values like the slope, y-intercept, and additional regression statistics.

How Do I Interpret the Results from LINEST?

Interpreting results from LINEST involves understanding key outputs like the slope and intercept, which indicate how much the dependent variable is expected to change with the independent variable. Additional metrics like R-squared tell us how well the data fits the model. High R-squared values generally imply a better fit, but context and data assumptions are vital for accurate interpretation.

Can LINEST Be Used for Non-Linear Models?

Yes, LINEST can handle polynomial regression, making it versatile for non-linear models as well. By transforming the independent variable into higher powers, you can fit a curve to the data. However, it’s crucial to ensure the model aligns with the underlying relationship to avoid overfitting.

How Does LINEST Function Compare to Other Excel Data Analysis Tools?

LINEST stands out in Excel for its specificity to linear regression without the need for additional toolpak installations. Compared to other tools like the Analysis ToolPak or built-in scatter plot trendlines, LINEST offers a balance between simplicity and analytical depth. While the Analysis ToolPak provides a broader range of statistical tests, LINEST is ideal for focused, linear analysis accessible directly within the worksheet.

How to do linear function on Excel?

To perform a linear function in Excel, typically you’d use the FORECAST.LINEAR function for a simple prediction or LINEST for a more detailed analysis. For a simple linear forecast, enter =FORECAST.LINEAR(x, known_y's, known_x's) into a cell, with x being the point you want to predict. For LINEST, you’d use the formula =LINEST(known_y's, known_x's) and press Ctrl+Shift+Enter if you’re including multiple ranges.