How to Find Any Nth Root in Excel Fast – Step by Step Guide

In this article, I’ll walk you through the steps to calculate the nth root of a number in Excel. Let’s dive in!

Key Takeaways:

• Use the POWER function or the caret operator (^) to calculate nth roots in Excel effectively.
• Enclose fractional exponents like 1/n in parentheses to ensure accurate calculations.
• Odd roots of negative numbers yield real results, while even roots require positive inputs to avoid errors.
• Use the ABS function for negative numbers and apply a negative sign for odd roots to maintain accuracy.
• Resolve errors like #NUM! or #VALUE! by checking formula syntax, cell references, and input validity.

 

Unlocking the Power of Excel for Advanced Roots

Understanding Nth Roots in Mathematical Terms

When delving into the capabilities of Excel, it’s crucial to have a firm grasp of mathematical concepts like nth roots. Simply put, the nth root of a number is that value which, when raised to the power of n, yields the original number. Think of it as the inverse operation of raising a number to a power.

For instance, if I’m looking to find the cube root of 27, I am searching for a number that when raised to the third power equals 27. It turns out to be 3, because 3^3 equals 27. In algebra, this operation is streamlined by representing the nth root of a number as the number raised to the fractional exponent of 1/n.

This mathematical operation isn’t just sot5me arcane piece of trivia; it’s a fundamental part of more complex equations and various applications in fields ranging from physics to finance.

Understanding the Formula for Nth Root

In Excel, we can use the POWER function or the caret operator (^) to calculate this. Both approaches yield the same result. Here’s the syntax:

• Using POWER Function: =POWER(number, 1/n)
• Using the Caret Operator: =number^(1/n)

Let me show you how to apply these in practice.

 

Swiftly Calculating the Nth Root with Excel Functions

Nth Root Precision with the POWER Function

The POWER function in Excel is a precise tool I utilize for nth root calculations. It allows me to raise any number to the power of 1/n effectively to find the nth root. This function is beautifully straightforward, yet powerful.

To calculate the square root, cube root, or any other nth root, the POWER function requires two arguments — the number and the power to which it is raised, which for roots, will be a fractional value.

=POWER(number, 1/n)

The POWER function is intuitive and easy to use. Here’s how:

STEP 1: Click on the cell where you want the result to appear.

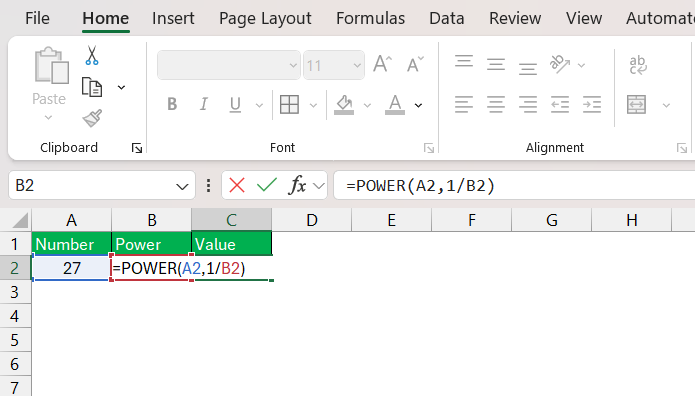
STEP 2: Enter the Formula: Type the formula =POWER(A2, 1/B2), where:

• A2 contains the number for which you want to calculate the nth root.
• B2 contains the value of “n” (the root).

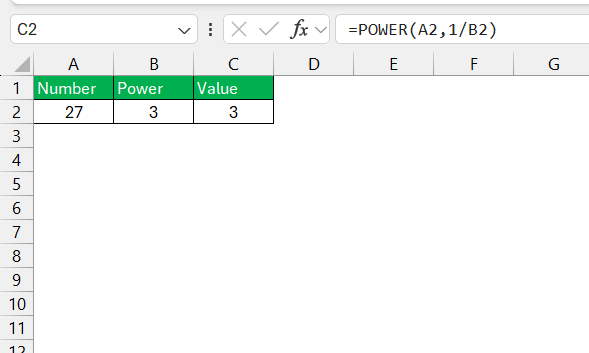
STEP 3: Excel will compute the result instantly.

For example, if A2 contains 27 and B2 contains 3, the formula will return 3, as the cube root of 27 is 3.

Utilizing the Exponent Operator (^) for Quick Results

The exponent operator (^) in Excel is another tool at my disposal for efficient nth root calculations. It’s a quicker way to compute roots without reaching out to specific functions. For instance, if I’m looking to find the fourth root of 16, I input =16^(1/4) directly into a cell to instantly obtain the result.

The caret operator is another simple method. Follow these steps:

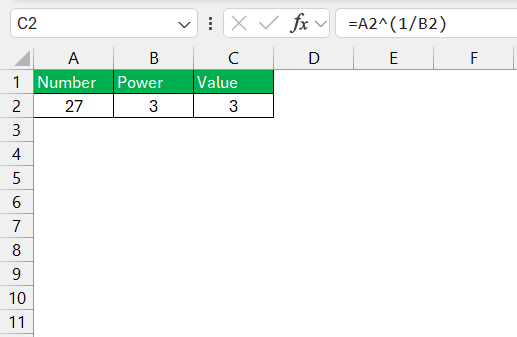
STEP 1: Click on the cell where you want to calculate the nth root.

STEP 2: Type =A2^(1/B2).

Excel will compute the nth root of the number. This method is particularly useful if you prefer a shorter formula.

 

Special Cases in Nth Root Calculations

Handling Nth Roots for Negative Numbers

Handling nth roots for negative numbers in Excel requires a bit more attention to detail. Generally, raising a negative number to a fractional power may lead to a complex number. However, if I’m looking for a real number as a result, it’s crucial to know that only odd roots of negative numbers are real numbers.

In Excel, I use the ABS function first to convert the negative number to its absolute positive equivalent. Then, I can use either the POWER function or the exponent operator (^), followed by applying a negative sign to the result if I’m dealing with an odd root.

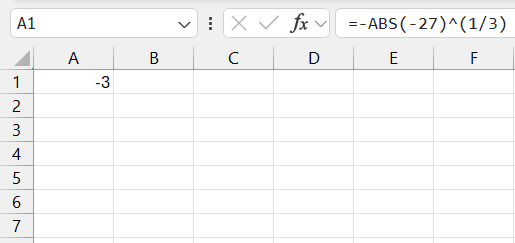
For example, to find the cube root of -27, the formula would be =-ABS(-27)^(1/3) which will correctly return -3.

Using this approach ensures that I don’t inadvertently acquire an error or a complex number when a real number is expected. It is a quick fix that enables Excel to handle an otherwise mathematically tricky situation and maintains the integrity of real-number calculations in my worksheet.

Tips for Dealing with Fractional and Irrational Numbers

When it comes to fractional and irrational numbers, I am aware that they can be tricky to work with in Excel due to their infinite or non-repeating nature. However, Excel is designed to handle these numbers up to a significant degree of precision.

For fractional numbers, particularly those representing roots, I use the POWER function or the exponent operator with carefully placed parentheses to maintain the correct order of operations.

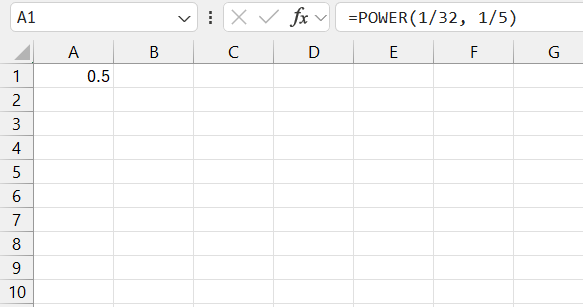
For example, if I want to calculate the 5th root of 1/32, which is a fractional number, I use =POWER(1/32, 1/5) or (1/32)^(1/5). Excel computes these fractional exponents with considerable accuracy.

As for irrational numbers like the square root of 2 or pi, I often use Excel built-in constants (such as PI()) or a large number of decimal places to represent them with sufficient precision for most practical purposes.

These numbers, when used within root calculations, should be rounded only at the end of all computations to ensure the final result retains as much accuracy as necessary.

To mitigate any complication with fractional and irrational numbers, I also use Excel’s formatting options to control the number of decimal places displayed, offering a balance between precision and readability in my spreadsheets.

 

Troubleshooting Common Issues with Nth Roots in Excel

Resolving Error Messages During Calculation

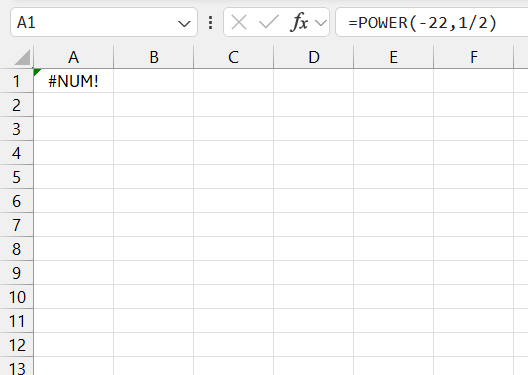
When faced with error messages during nth root calculations in Excel, I take a systematic approach to resolve them. The ‘#NUM!’ error often appears if I attempt to calculate an even root of a negative number, as real results do not exist for this scenario.

To address this, I ensure I’m either working with a positive number or adjusting the root to an odd number.

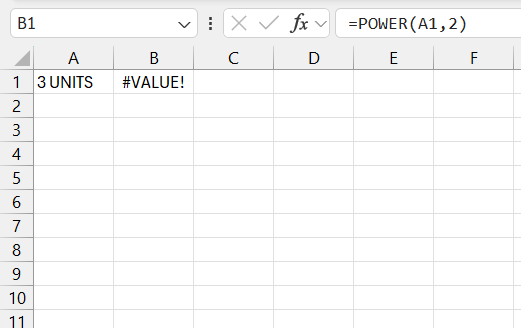
‘VALUE!’ error messages, on the other hand, flag that Excel doesn’t recognize the input as numeric. This could be due to formatting issues or incorrect formula syntax.

I carefully check the cell’s format and re-enter the formula or data correctly.

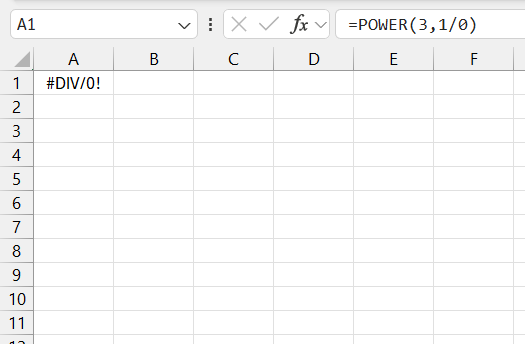
If I encounter the ‘#DIV/0!’ error, it indicates that I am attempting to divide by zero, which happens if my formula includes a zero in a denominator or an incorrect cell reference leading to a zero-value.

It’s essential to review the references and inputs to make sure they return a non-zero value.

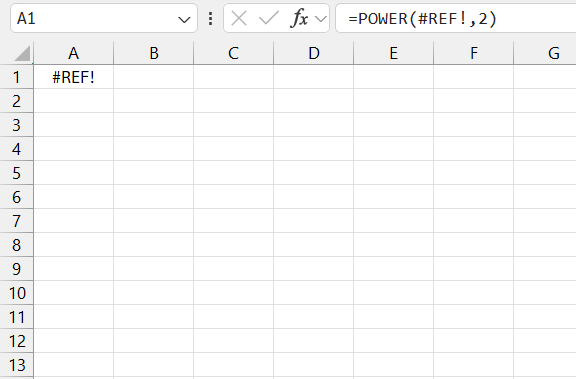
I also keep an eye for the ‘#REF!’ error, which screams that a reference is invalid. Perhaps because I’ve deleted a cell or an entire row/column that was part of my formula.

To fix it, I either undo the deletion or update the formula to reference the correct cells.

To nip these issues in the bud, I also exploit Excel’s built-in ‘Error Checking’ feature that helps in pinpointing and guiding the correction process.

 

FAQ: Mastering Nth Roots in Excel

How to calculate the nth root?

To calculate the nth root of a number in Excel, use the =number^(1/n) formula, where number is the base number and n is the degree of the root. For instance, to find the 5th root of 32, enter =32^(1/5) into a cell, and Excel will display the result. Make sure to place parentheses around 1/n to get the correct order of operations.

What is the syntax for calculating an Nth root using the POWER function?

The syntax for calculating an nth root using the POWER function in Excel is =POWER(number, 1/n). Replace number with the base number and n with the root you wish to calculate. For example, to find the cube root of 8, the formula would be =POWER(8, 1/3). Remember to enclose 1/n in parentheses to ensure accurate calculation.

Can Excel calculate Nth roots for negative numbers, and if so, how?

Yes, Excel can calculate nth roots for negative numbers, but only for odd roots which result in real numbers. The formula is =-ABS(number)^(1/n), where number is the negative base number and n is an odd integer. For example, for the cube root of -27, the formula would be =-ABS(-27)^(1/3), which yields -3.

Are there any shortcuts to enter the POWER function quickly in Excel?

There aren’t specific shortcuts for entering the POWER function in Excel, but you can quickly insert functions by pressing Alt + = to autosum a column, which activates the formula bar, then type “POWER” and continue with your formula. Also, familiarizing yourself with ‘Ctrl’ + ‘Shift’ + ‘L’ to toggle filters and ‘Ctrl’ + ‘Arrow keys’ to navigate, helps in speeding up data entry before formula use.

How can I overcome errors when calculating Nth roots in Excel?

To overcome errors when calculating nth roots in Excel, ensure your number is positive when calculating even roots, enclose the 1/n expression in parentheses, and recheck cell references. Use the IFERROR function to handle potential errors gracefully and give alternative results or messages, making troubleshooting more straightforward.