How to Use Pythagorean Theorem in Excel – Step by Step Formula Guide

The Pythagorean Theorem is one of those mathematical principles that you don’t realize how often you use until you’re knee-deep in a project. Whether you’re calculating distances, working on geometry problems, or building something practical, it always seems to find a way into your work. For me, bringing this classic theorem into Excel has saved me countless hours. Let me show you how I use Excel to handle Pythagorean Theorem calculations.

Key Takeaways:

• Excel simplifies Pythagorean Theorem calculations using built-in functions like SQRT and exponentiation.
• Setting up a structured spreadsheet layout ensures accuracy and ease of use for triangular calculations.
• Excel’s formulas can be adjusted to find missing sides, not just the hypotenuse.
• The Law of Cosines extends Excel’s capabilities to non-right triangles, enhancing its mathematical applications.
• Error handling techniques like IFERROR help troubleshoot formula mistakes and improve workflow.

 

Unraveling the Mystery of the Pythagorean Theorem in Excel

What is the Pythagorean Theorem?

Let’s quickly recap the theorem. It states that in a right triangle, the square of the hypotenuse (“c”) is equal to the sum of the squares of the other two sides (“a” and “b”). The formula looks like this:

c² = a² + b²

If you’re solving for the hypotenuse, you rearrange it to:

c = √(a² + b²)

Excel makes it simple to calculate this without having to dust off your calc

A Perfect Pair for Problem Solving

Excel isn’t just for financial analysts; it’s a robust tool for mathematicians and educators too. Its grid-like structure mimics graph paper, making it ideal for visualizing and solving mathematical problems, including those involving the Pythagorean Theorem. Excel’s cell references and built-in functions allow for dynamic calculations that update automatically with every change in input values.

This feature is particularly advantageous when exploring multiple scenarios or conducting what-if analyses. By harnessing Excel’s capabilities, solving complex mathematical problems, such as finding the length of the hypotenuse or the legs of right-angled triangles, becomes a structured and engaging process for students and professionals alike.

 

Quickstart Tutorial: Applying Pythagorean Theorem in Excel

Setting Up Your Excel Spreadsheet for Triangular Calculations

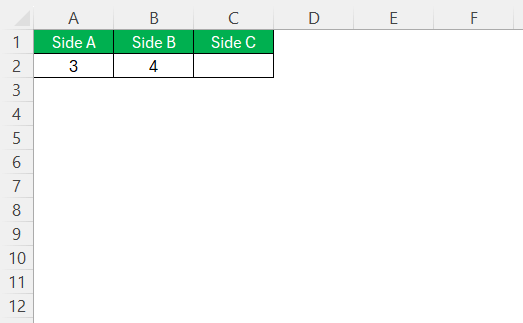
Setting up an Excel spreadsheet for triangular calculations involves a series of thoughtful steps that facilitate ease of use and accuracy. First, it’s essential to design a clear layout. Label columns for the different sides of the triangle—usually ‘a,’ ‘b,’ for the legs, and ‘c’ for the hypotenuse. Input known values into the respective cells.

If working with numerous triangles, ensure that there’s a clear distinction between each set of values—using separate rows can help. Next, reserve cells where Excel will display the results of your calculations, and consider color-coding or bolding these for quick reference. Finally, verify that the spreadsheet is set to the correct unit of measurement, matching the data you will be entering.

Enter the Formula: Computing Hypotenuse and Legs with Ease

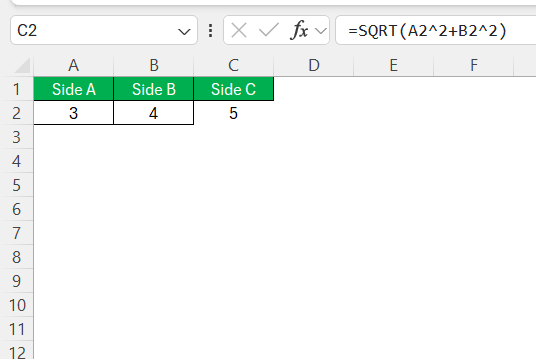
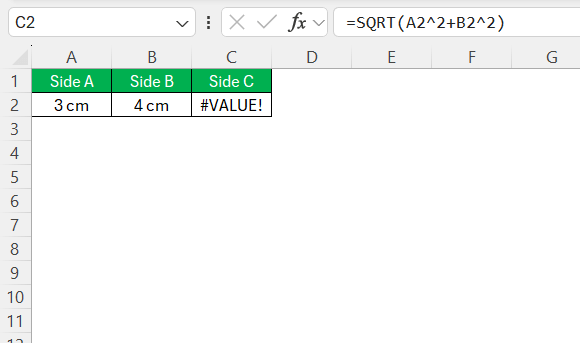
To compute the length of the hypotenuse with ease, make use of Excel’s SQRT and exponentiation (^) functions. For example, let’s say cells A2 and B2 contain the lengths of the legs ‘a’ and ‘b,’ respectively. In cell C2, which is reserved for the hypotenuse ‘c,’ I would enter the formula “=SQRT(A2^2+B2^2)”.

Instantly, Excel carries out the square of both values, adds them together, and finds their square root, providing the length of the hypotenuse.

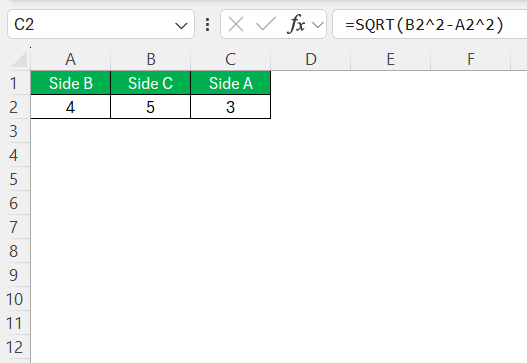
If I want to reverse the process and calculate one of the legs when I know the hypotenuse and the other leg, the formula would need a slight adjustment to subtract the square of one leg from the square of the hypotenuse before finding the square root.

a = √(c² – b²)

For clarity and to minimize errors, use parentheses to group the operations correctly.

 

Beyond the Basics: Advanced Pythagorean Applications in Excel

Dealing with Non-Right Triangles: How Excel Can Still Help

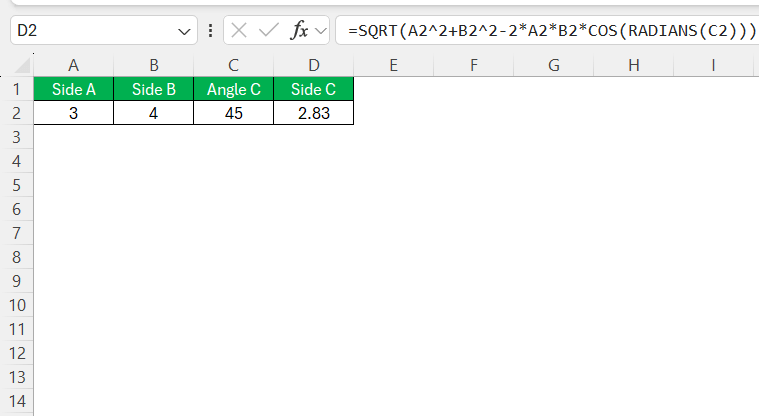
Even when faced with non-right triangles, Excel remains a helpful companion. While the Pythagorean Theorem exclusively applies to right-angled triangles, Excel can still assist in these cases by employing the Law of Cosines, an extension of Pythagorean principles to non-right triangles.

For a triangle with sides of length ‘a,’ ‘b,’ and ‘c,’ and an angle ‘C’ opposite side ‘c,’ the formula “=SQRT(A2^2 + B2^2 – 2*A2*B2*COS(RADIANS(C2))” provides the length of side ‘c.’ Replace A2, B2, and C with the appropriate cell references and angle measurements.

The ability to input trigonometric functions like COS is one of the many ways Excel proves its worth beyond the basics of the Pythagorean Theorem. Always remember, however, that the angle must be in radians or converted to radians using the RADIANS function within Excel.

 

Troubleshooting Common Issues when Using Pythagorean Theorem in Excel

Error Messages Decoded: Making Sense of Excel’s Feedback

Deciphering Excel’s error messages is crucial to maintaining workflow and ensuring accurate computations. Common messages like #VALUE! often indicate a non-numeric input where a number was expected; double-check that all side lengths are numeral.

A #NUM! error highlights an issue with a formula, such as taking the square root of a negative number when calculating a triangle side—be sure your triangle dimensions make geometrical sense.

Remember, the #DIV/0! error signifies a division by zero, a situation that shouldn’t occur in Pythagorean calculations but might arise if mistakenly using the wrong formula.

For clean error handling, use Excel’s IFERROR function to specify an alternative result or message if an error is detected.

Checking for Accuracy: Ensuring Correct Data Entry and Formula Use

Ensuring accuracy in Excel’s Pythagorean calculations is twofold: verifying both data entry and correct formula use. To avoid common mistakes, always double-check the side lengths entered against source data. Be vigilant for accidental spaces or non-numeric characters which can cause errors or incorrect results.

When it comes to formulas, ensure that each component is in the correct order and that parentheses are properly used to structure the calculations. Utilize Excel’s built-in “Trace Precedents” and “Trace Dependents” features to visualize formula relationships and data flow. For good measure, I always perform spot checks with manual calculations or a reliable secondary method. Cross-referencing results increases confidence in the spreadsheet’s accuracy.

 

Maximizing Excel Features for Enhanced Pythagorean Computations

Using Functions and Formulas: A Deeper Dive into Excel’s Capabilities

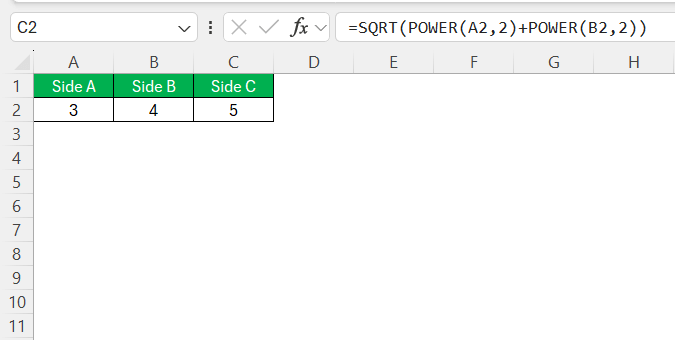
Venturing deeper into Excel’s treasure trove of functionality, I often encounter various functions that can be ingeniously applied to Pythagorean calculations. Beyond basic arithmetic operators, functions like POWER (for squaring values) and ABS (to handle absolute values) help refine formula construction.

For example, instead of using the caret (^) for exponentiation, I can use “=SQRT(POWER(B5,2)+POWER(C5,2))” to calculate the hypotenuse.

This can be especially effective when building complex formulas, providing clarity and precision. Excel also allows for the creation of custom formulas, enabling the encapsulation of the entire Pythagorean process into a single, reusable function—this is a pinnacle of its capabilities that can save valuable time.

 

Tips and Tricks: Streamlining Your Pythagorean Calculations in Excel

Keyboard Shortcuts and Productivity Hacks for Quicker Results

In my quest for efficiency, mastering keyboard shortcuts in Excel has been a game-changer, particularly when working with the Pythagorean Theorem. Shortcuts like Ctrl + C for copying, Ctrl + V for pasting, and Ctrl + Z for undoing mistaken actions, are just the tip of the iceberg. To enter and edit formulas rapidly, I use F2 to edit the active cell, and Ctrl + Shift + Enter to input array formulas, which can be invaluable for handling complex data sets.

For those often-used functions, like SQRT, creating named ranges and using the Name Manager can save clicks and typing time. Additionally, customizing the Quick Access Toolbar to include the most frequently used tools places them right at my fingertips, further speeding up my workflow. Embracing these productivity hacks yields quicker results and transforms the user experience from labor-intensive to smooth sailing.

FAQ: Mastering Pythagorean Theorem in Excel

How to make Pythagoras theorem in Excel?

To use the Pythagoras theorem in Excel, input the lengths of two sides of a right-angled triangle and apply the formula a^2 + b^2 = c^2 in a cell. For the hypotenuse ‘c’, enter “=SQRT(A2^2 + B2^2)” assuming ‘A2’ and ‘B2’ contain the side lengths. Excel calculates the square root of the sum of squares, giving you the length of the hypotenuse.

Can I use Excel to solve for missing triangle sides other than the hypotenuse?

Yes, you can rearrange the formula to solve for a missing leg by using =SQRT(C5^2 - B5^2), where C5 is the hypotenuse and B5 is the known leg.

How do I ensure my Pythagorean calculations are accurate in Excel?

Double-check data entry, use parentheses correctly in formulas, and cross-verify with manual calculations or another tool. Excel’s “Trace Precedents” feature also helps visualize formula dependencies.

What should I do if I get an error when calculating the hypotenuse?

A #VALUE! error usually means a non-numeric input, while a #NUM! error could indicate an invalid square root operation. Use IFERROR to handle mistakes gracefully.

Can Excel handle calculations for non-right triangles?

Yes, you can use the Law of Cosines formula in Excel: =SQRT(A2^2 + B2^2 - 2*A2*B2*COS(C2)), ensuring the angle is in radians by using the RADIANS function.