The Ultimate Guide to Quadratic Formula Solver in Excel

Mastering the quadratic formula solver in Excel opens up a world of possibilities for efficiently handling quadratic equations in a variety of contexts. Excel’s powerful calculation and function capabilities allow for precise numerical solutions, which are essential in fields like finance, engineering, and environmental science. In mastering these tools, you will enhance your ability to tackle real-world problems with confidence and precision.

Key Takeaways:

• Excel enables clear organization and solving of quadratic equations by using separate cells for coefficients a, b, and c.
• The standard quadratic formula can be applied in Excel using cell references and built-in functions like SQRT.
• Goal Seek is useful in finding the value of x that satisfies ax² + bx + c = 0 without needing complex formulas.
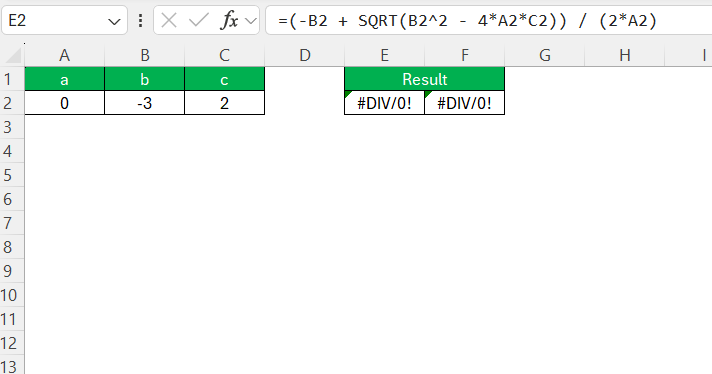
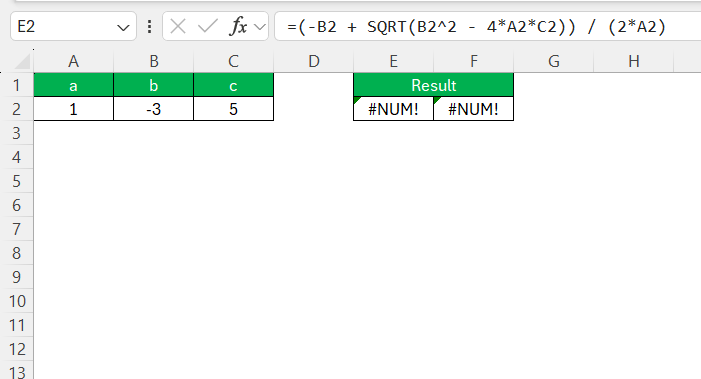
• Errors like #NUM! or #DIV/0! typically result from negative discriminants or zero denominators and can be corrected with careful checks.
• Quadratic equations have real-world applications in finance, engineering, and environmental science, where Excel simplifies modeling and analysis.

 

Setting Up Quadratic Equations in Excel

Manual Entry of Quadratic Data

Manually entering quadratic data into Excel is a straightforward process, but it requires careful attention to detail to ensure accuracy. Begin by setting up your spreadsheet with clearly labeled columns or rows for each component of the quadratic equation: the coefficients ‘a’, ‘b’, and ‘c’. This step is crucial as these coefficients define the specific quadratic equation you are analyzing.

Enter each coefficient into its respective cell. It’s a good practice to use a separate column or row for each quadratic equation you plan to solve. For example, if you are working on multiple equations simultaneously, label a new row for each equation with its corresponding coefficients. This organized system helps in managing and comparing multiple equations systematically.

In addition to coefficients, you may wish to add a row or column for the results of your calculations, such as the calculated roots. By setting up your spreadsheet for clear and clean data entry, you prepare the foundation for efficient and effective problem-solving.

 

Master Quadratic Formula Solver in Excel

The Standard Quadratic Formula

The standard quadratic formula is a fundamental tool for solving quadratic equations and is applicable when the equation is in the form ax² + bx + c = 0, where ‘a’, ‘b’, and ‘c’ are constants with ‘a’ not equal to zero. The solutions, or roots, of the equation are given by:

x = (-b ± √(b² – 4ac)) / 2a

This formula provides the two potential values for x that satisfy the equation due to the plus/minus symbol (±), which indicates that you must perform the calculation twice — once with addition and once with subtraction.

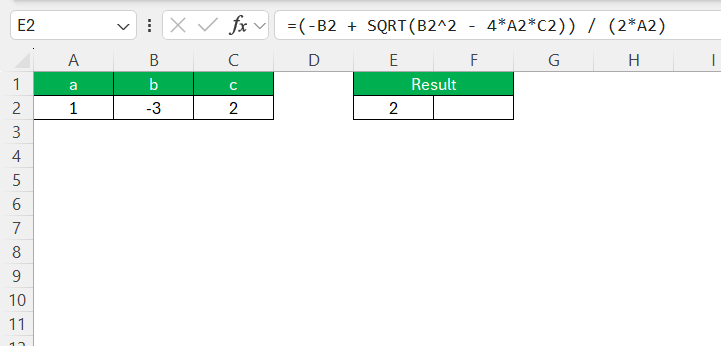
To implement this in Excel, you can use the formula syntax directly in a cell. First, ensure your spreadsheet has cells assigned for the coefficients of the equation. Then, input the quadratic formula to find the roots by referencing those cells. For instance, if coefficients ‘a’, ‘b’, and ‘c’ are in cells A2, B2, and C3, respectively, the formula for one root would be:

=(-B2 + SQRT(B2^2 – 4*A2*C2)) / (2*A2)

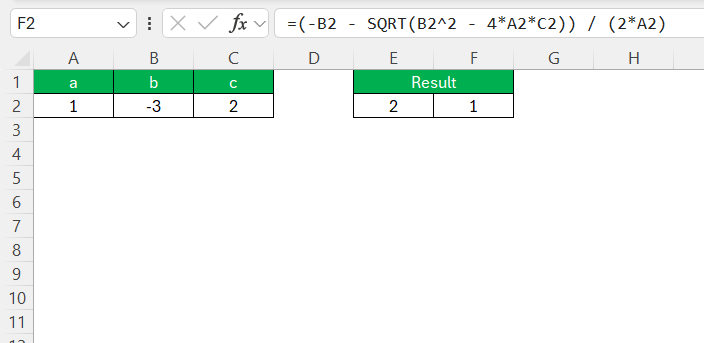
Similarly, for the other root, change the plus to a minus:

=(-B2 – SQRT(B2^2 – 4*A2*C2)) / (2*A2)

This method allows Excel to automatically compute the roots of the quadratic equation using the provided coefficient values. Ensure the values under the square root (the discriminant, b² – 4ac) are not negative, as this would result in complex numbers which standard Excel functions can’t handle without additional configurations. By following this procedure, you leverage Excel’s calculation power to solve quadratic equations efficiently.

Step-by-Step Guide to Goal Seek

Goal Seek is a powerful Excel tool that assists in finding the correct variable input needed to achieve a desired outcome in formulas, particularly useful for quadratic equations. Here’s a step-by-step guide to leveraging Goal Seek for solving these equations:

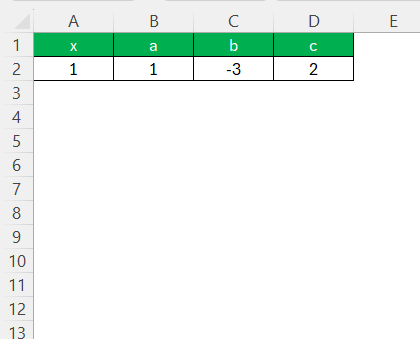
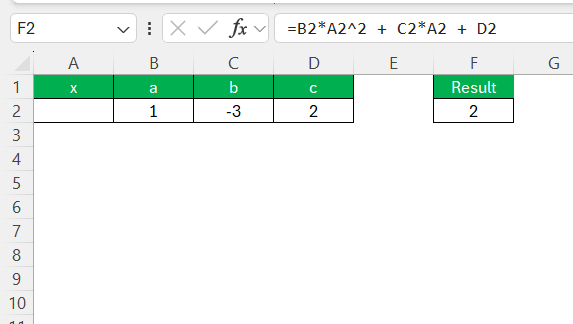
STEP 1: First, ensure your quadratic equation ax² + bx + c = 0 is prepared in the spreadsheet. Designate a cell to contain the formula, substituting coefficients ‘a’, ‘b’, ‘c’ and variable ‘x’ with appropriate references.

STEP 2: Choose a cell to serve as your formula cell where you’ll compute the value of the quadratic equation. For example, use =B2*A2^2 + C2*A2 + D2 if A2 is where you guess the value of x and B2, C2, D2 contain coefficients a, b, c.

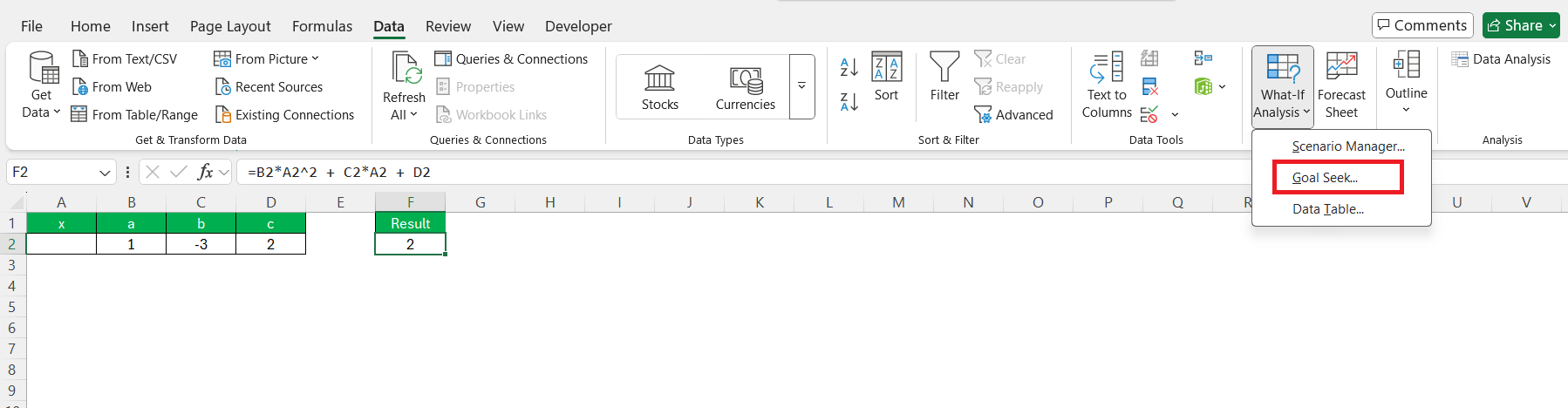
STEP 3: Navigate to the Data tab, then to Data Tools, and select “What-If Analysis” followed by “Goal Seek.”

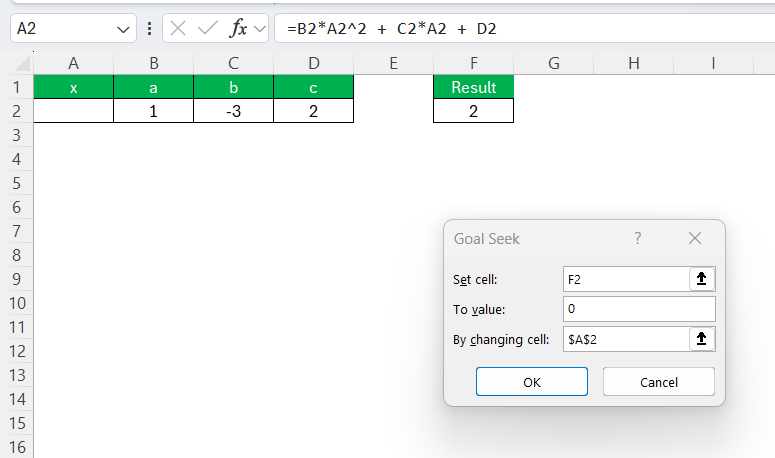
STEP 4: In the Goal Seek dialog:

• Set ‘Set Cell’ to the formula cell.
• Assign ‘ToValue’ to 0, as you aim to find the root where the equation equals zero.
• Under ‘By changing cell’, select the cell containing the guessed x value (e.g., A1).

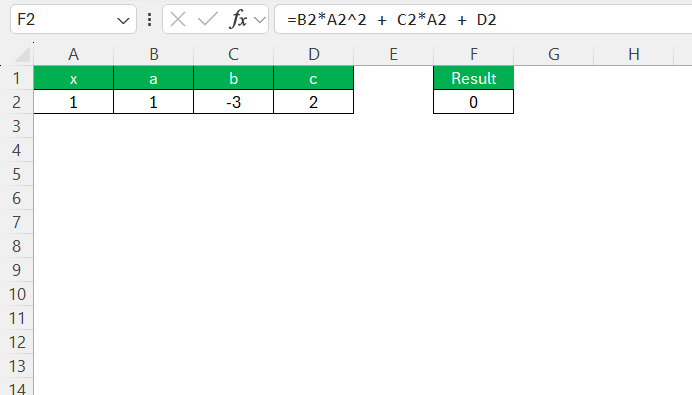
STEP 5: Click OK to start the Goal Seek operation. Excel will iterate through potential values for x to find the one that makes the equation’s result as close to zero as possible.

Goal Seek iteratively adjusts the x value to minimize the equation’s output within its default precision limits, which may require manual intervention for refining precision. Ensure your initial guess is reasonable to improve the chances of Goal Seek converging on an accurate solution efficiently. This method effectively automates finding solutions without needing complex programming, making it a practical tool for quick problem-solving in quadratic equations using Excel.

 

Troubleshooting Common Errors

While solving quadratic equations in Excel, encountering errors is not uncommon. Understanding how to troubleshoot these issues is crucial:

Error Values (#VALUE!, #DIV/0!): Ensure all cells contain appropriate numeric values. For #DIV/0!, verify that ‘a’ (denominator in the quadratic formula) is not zero. Double-check the data inputs for consistency and accuracy.

Complex Roots: If the discriminant (b² – 4ac) is negative, Excel will return #NUM! because it does not solve complex numbers natively. Consider using a different tool or workaround involving separate calculations for real and imaginary parts.

Goal Seek Limitations: Goal Seek might struggle with equations that have multiple solutions or complex roots. If Goal Seek fails to find a solution, try different starting values for x or use Excel’s Solver tool for more comprehensive analyses.

By recognizing these common pitfalls and employing appropriate solutions, users can navigate troubleshooting efficiently. Regular formula verification and attentive data management further aid in preventing and resolving errors promptly. These measures not only enhance the accuracy of your problem-solving process in Excel but also improve your overall experience with the platform, enabling you to tackle quadratic equations confidently and effectively.

By maintaining vigilance and applying troubleshooting strategies, you ensure a smoother calculation process, even when complex or unexpected issues arise.

 

Practical Applications in Real Life

Finance: Calculating Investment Returns

In finance, quadratic equations can be instrumental in calculating and assessing investment returns. Particularly, they aid in modeling investment portfolios, analyzing the cost of capital, and forecasting potential financial trends. By applying these mathematical models, finance professionals can make informed predictions regarding the potential growth or decline of investment returns over time.

One practical application is using quadratic equations to estimate the Internal Rate of Return (IRR), which often involves seeking a rate that equates the present value of expected future cash flows with the initial investment cost. The iterative approach allowed by Excel’s Goal Seek or Solver functions, supplemented by AI-driven analytics, can speed up the calculation process compared to manual evaluations.

Furthermore, quadratic models can help determine the optimal portfolio balance by evaluating risk and return trade-offs. They assist analysts in identifying the right balance between high-risk, high-return investments and lower-risk ones, thus optimizing returns while managing risk. Leveraging quadratic equations in finance provides a powerful toolset for professionals aiming to enhance strategic decision-making and maximize investment performance over time.

Engineering: Load and Stress Analysis

In engineering, quadratic equations play a crucial role in load and stress analysis, which is vital for ensuring the safety and reliability of structures and materials. Engineers use these equations to model how forces such as tension, compression, and bending impact different structural components, facilitating precise calculations of stress and deflection.

For instance, when designing bridges, buildings, or mechanical parts, engineers must predict how materials will respond to varied loads without failing. Quadratic equations help in determining the critical points where stress could cause structural failure. By inserting load parameters into these equations, engineers can derive solutions that predict whether a structure can withstand specific stresses and identify areas that might require reinforcement.

Additionally, quadratic equations assist in optimizing material use, ensuring that designs are not only safe but also cost-effective. By accurately calculating the maximum stress a material can endure, engineers can select materials that meet safety standards while considering economic constraints. Excel, with its computational capabilities, allows for streamlined calculations of these quadratic models, thus facilitating efficient engineering analysis and design iterations.

Environmental Science: Analyzing Chemical Reactions

In environmental science, quadratic equations are pivotal in analyzing chemical reactions, particularly when modeling reaction rates and equilibrium processes. These equations help scientists predict how chemicals interact under various conditions, which is essential for understanding environmental impacts and developing sustainable solutions.

One application is in determining the equilibrium concentrations of reactants and products in a closed system. By setting up a quadratic equation based on the reaction’s stoichiometry and equilibrium constant, scientists can solve for unknown concentrations. This analysis aids in assessing environmental processes such as acid-base neutralization, pollutant formation, or nutrient cycling in ecosystems.

Furthermore, quadratic equations assist in modeling the kinetics of reactions, such as how quickly pollutants degrade or transform in the environment. By analyzing these rates, scientists can predict the persistence of harmful compounds, informing remediation strategies and policy decisions.

Excel’s computational tools support environmental scientists by providing a platform for complex calculations and scenario testing, enhancing their ability to simulate and analyze chemical reactions efficiently. Mastery of these equations in Excel allows for better-informed decisions regarding environmental protection and resource management.

 

FAQs

What is a quadratic equation?

A quadratic equation is a type of polynomial equation that features a variable raised to the power of two, having the form ax² + bx + c = 0. Here, ‘a’, ‘b’, and ‘c’ are constants with ‘a’ not equal to zero, as this ensures the equation remains quadratic rather than linear. The solutions, known as roots, may be real or complex numbers, and they represent the values of ‘x’ that satisfy the equation. Quadratic equations are foundational in algebra and have varied applications across mathematics, science, and engineering.

How do I input a quadratic formula into Excel?

To input a quadratic formula into Excel, start by setting up cells for the coefficients ‘a’, ‘b’, and ‘c’. For example, place ‘a’ in A1, ‘b’ in B1, and ‘c’ in C1. Then, for the roots, use the quadratic formula:

• For the positive root, enter: =(-B1 + SQRT(B1^2 - 4*A1*C1)) / (2*A1).
• For the negative root, use: =(-B1 - SQRT(B1^2 - 4*A1*C1)) / (2*A1).

These formulas calculate the solutions based on your input coefficients.

What should I do if Excel shows an error like #NUM! when solving a quadratic equation?

A #NUM! error usually means that the discriminant (b² – 4ac) is negative, leading to complex roots that Excel can’t handle natively. You can avoid this by checking your coefficients and ensuring the discriminant is non-negative. If complex solutions are necessary, consider separating real and imaginary parts manually or using external tools like MATLAB or Python for more advanced computation.

How is Goal Seek different from using the quadratic formula in Excel?

The quadratic formula provides an exact, formula-based solution to find the roots, but it may fail if there’s an input or syntax error. Goal Seek, on the other hand, is an iterative method that guesses the correct value for x that brings the equation result close to zero. While it’s more flexible and doesn’t need the quadratic formula, it may need a good initial guess and doesn’t work well with equations having multiple or complex roots.

Is there a quadratic formula solver in Excel?

Excel does not have a built-in quadratic formula solver specifically labeled as such, but you can solve quadratic equations using its functions and tools. By employing the quadratic formula with Excel’s arithmetic and SQRT functions, you can compute the roots manually. Additionally, tools like Goal Seek and Solver allow you to iteratively solve equations by finding root approximations, which can act as a “solver” for practical purposes.