The Ultimate Guide to Spearman Correlation in Excel – Rank Correlation Guide

While working with data, you might come across scenarios where determining the strength and direction of the relationship between two variables becomes important. This is where the Spearman correlation, a non-parametric measure of rank correlation, comes into play. Let me guide you through the process of calculating Spearman correlation in Excel.

Key Takeaways:

• Spearman correlation assesses rank-based relationships, which is ideal for non-linear or ordinal data.
• Ranking data is crucial for Spearman correlation, using tools like Excel’s RANK.AVG.
• Calculations involve ranking, finding rank differences, squaring them, and applying a specific formula.
• Spearman works well with non-linear relationships and is robust against outliers.
• Real-world applications span psychology, finance, healthcare, and environmental studies.

 

Harnessing Data Relationships with Spearman Correlation

What is Spearman Correlation?

Spearman correlation, also known as Spearman’s rank correlation coefficient, is a non-parametric measure of the strength and direction of the relationship between two variables. Unlike Pearson correlation, which requires data to be linear and normally distributed, Spearman correlation works on ranked data, making it ideal for ordinal data or non-linear relationships.

Understanding the Importance of Ranking Data

When we delve into statistical analysis, understanding the relationships between different sets of data becomes vital. Spearman’s rank correlation coefficient offers us a window into these relationships by focusing on the ranks rather than the raw data. This approach is particularly useful when dealing with ordinal or non-parametric data, where the magnitude of difference between data points isn’t as important as the order of those points.

Imagine you are comparing customer satisfaction ratings with wait times at a restaurant. The raw scores might vary, but what Spearman correlation zeroes in on is whether a higher wait time consistently coincides with a lower satisfaction ranking, regardless of the numerical values involved.

 

Steps to Calculate Spearman Correlation in Excel

Prepare Your Data

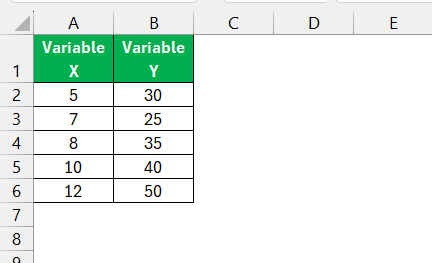
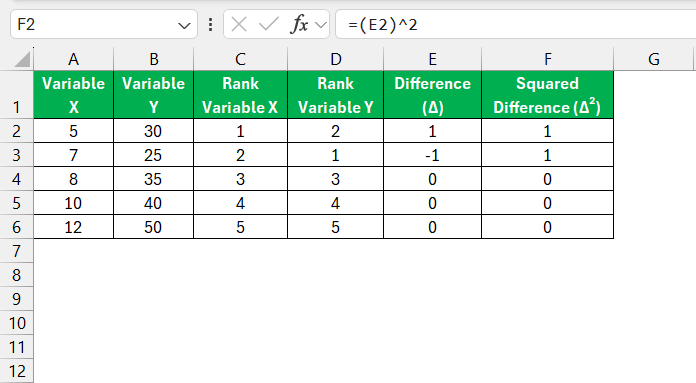
First, ensure that your dataset is organized in two columns—one for each variable you want to analyze. For example:

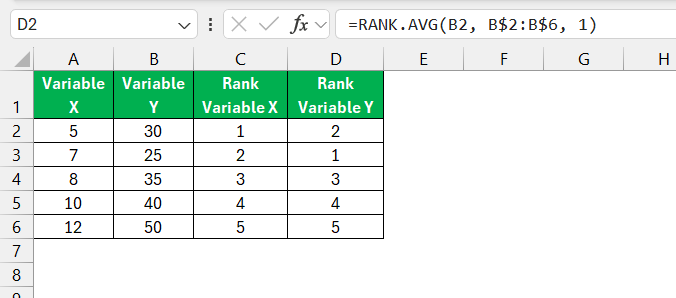
Rank the Data

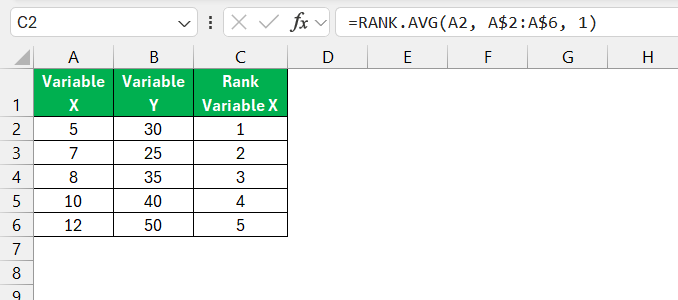
Spearman correlation requires you to rank the values in each variable. You can use Excel’s RANK.AVG function to handle this:

Rank Variable X: In a new column, use the formula:

=RANK.AVG(A2, A$2:A$6, 1)

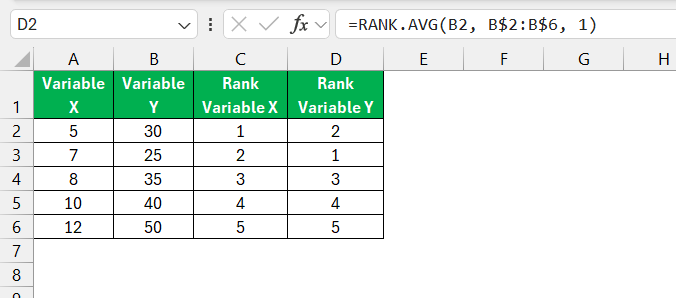
Rank Variable Y: In another column, use the formula:

=RANK.AVG(B2, B$2:B$6, 1)

You should now have ranked data for both variables.

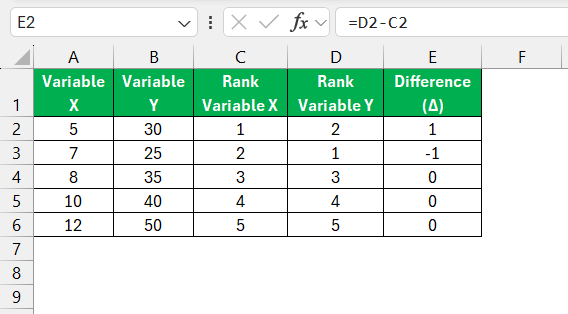
Calculate the Difference Between Ranks

Create a column for the difference (Δ) between the ranks of each variable:

=D2 – C2

Square the Differences

Create another column to square the differences (Δ²):

=(E2)^2

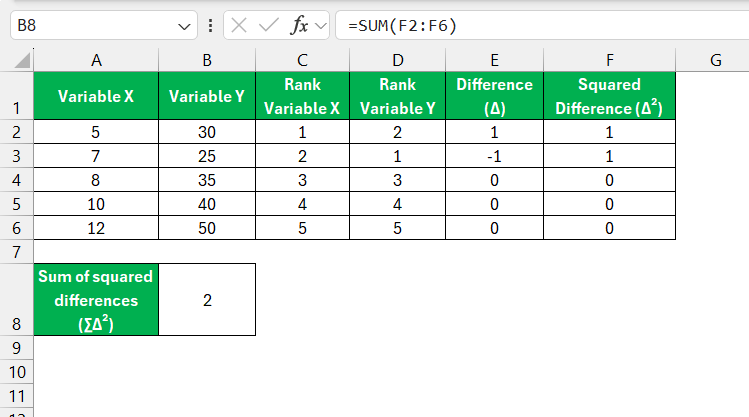
Sum the Squared Differences

At the bottom of the Δ² column, use the SUM function to calculate the total sum of squared differences (∑Δ²):

=SUM(F2:F6)

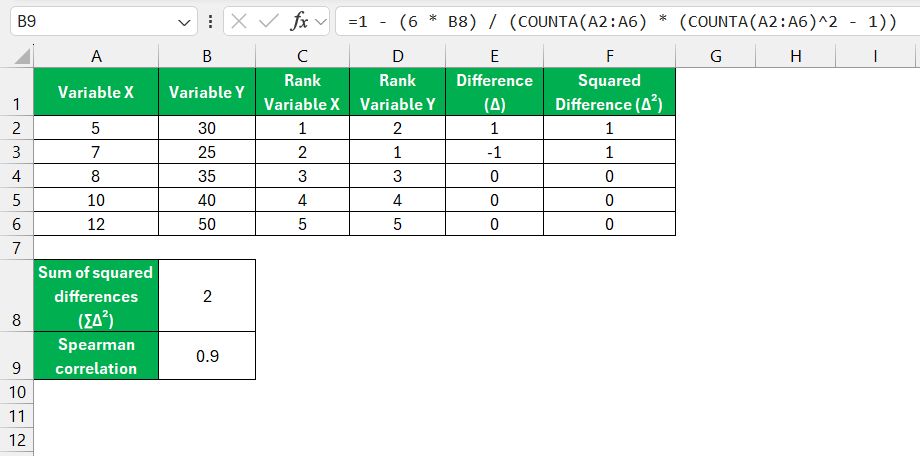
Apply the Spearman Correlation Formula

The formula for Spearman correlation (ρ) is:

Where:

• ∑di² is the sum of squared differences.
• n is the number of data points.

Use this formula in Excel:

=1 – (6 * B8) / (COUNTA(A2:A6) * (COUNTA(A2:A6)^2 – 1))

This will give you the Spearman correlation coefficient.

Interpreting the Result

The Spearman correlation coefficient ranges from −1 to 1:

• 1: Perfect positive correlation.
• 0: No correlation.
• −1: Perfect negative correlation.

A coefficient closer to 1 or −1 indicates a strong relationship, while a coefficient near 0 suggests a weak or no relationship.

 

Using Excel’s Data Analysis ToolPak

If manual calculations seem daunting, you can use the Analysis ToolPak add-in for statistical computations. Unfortunately, Excel doesn’t have a built-in Spearman correlation function, but you can calculate Pearson correlation on ranked data to achieve the same result.

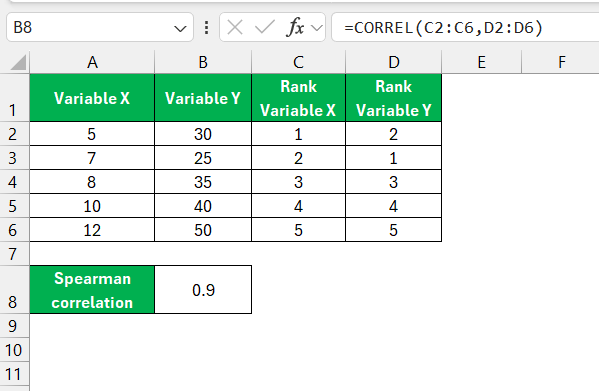
STEP 1: Rank Your Data by following the steps mentioned above.

STEP 2: Use the CORREL function to get the correlation coefficient.

=CORREL(C2:C6,D2:D6)

This gives you the Spearman correlation coefficient.

 

Advancing Your Skills: Spearman Correlation in Action

Real-world Applications Where Spearman Makes a Difference

Spearman correlation is a versatile tool that has tangible impacts across various fields. Let’s touch on a few real-world applications where Spearman correlation is particularly advantageous:

• In psychology, Spearman correlation helps analyze questionnaire data where responses are ranked on a Likert scale, revealing how variables like stress and sleep quality may be monotonically related.
• In education, it can uncover relationships between students’ ranks in different subjects, such as ranking in mathematics vs. natural sciences, offering insights for curriculum development.
• In finance, analysts use it to understand the relationship between the rank order of stock prices over different time frames, which can be crucial for portfolio management.
• In healthcare, Spearman correlation might correlate patient satisfaction rankings with hospital readmission rates, providing valuable feedback for hospital administrators.
• Environmental studies often employ Spearman to explore the relationship between the ranked order of pollutant levels and the incidence of certain diseases within a population.

These examples highlight Spearman’s ability to decipher rank-based relationships, providing clarity even when data distributions are unconventional or nonlinear. By using Spearman correlation, professionals across these fields can derive insights that inform decisions, drive policy changes, and shape strategic directions.

FAQ: Master Spearman Correlation in Excel Made Simple

How to calculate Spearman correlation?

To calculate Spearman correlation in Excel: Rank both data sets, find the difference between each pair of ranks, square those differences, sum all squared differences, and use the formula rs = 1 – (6 * Σd^2) / (n * (n^2 – 1)), where Σd^2 is the sum of squared rank differences, and n is the number of observations.

What are the advantages of using Spearman correlation over Pearson correlation?

Spearman correlation is more robust than Pearson as it doesn’t require assumptions of normality and linearity, making it ideal for ordinal data, non-linear relationships, or when outliers are present that could skew Pearson results.

How do I handle tied ranks when calculating Spearman correlation in Excel?

In Excel, use the RANK.AVG function to handle tied ranks which gives each tied value the average of the ranks they would cover; this ensures tied data points are assigned their proper rank, crucial for Spearman correlation accuracy.

Can Spearman correlation be used for non-linear relationships?

Yes, Spearman correlation is suitable for non-linear relationships because it assesses the monotonic relationship based on rank rather than the absolute values, making it ideal for data that doesn’t fit a linear model.

What does a Spearman correlation coefficient close to zero signify?

A Spearman correlation coefficient close to zero signifies that there is no apparent monotonic relationship between the ranked variables; the ranks do not increase or decrease consistently together.