Surface Area of a Cone in Excel – Step by Step Formula Guide

Calculating the surface area of a cone can be done quickly and efficiently in Excel. Whether you’re a student, engineer, or just someone looking to automate tedious calculations, Excel is a perfect tool for this. In this article, I’ll walk you through step-by-step on how to calculate the surface area of a cone in Excel using the appropriate formula.

Key Takeaways:

• Excel simplifies surface area calculations of cones using formulas like =PI()*A2*(A2 + SQRT(B2^2 + A2^2)).
• Understanding cone metrics—radius, height, and slant height—is crucial for accurate computations.
• The PI function in Excel ensures precision by providing π to 15 decimal places.
• You can calculate both the curved and total surface areas of a cone using Excel’s formula capabilities.
• Excel’s automation of repetitive tasks minimizes errors and speeds up complex calculations.

 

Introduction to Surface Area Calculations in Excel

Unraveling the Mystery of Cone Geometry

In my exploration of geometric forms, cones have always stood out with their unique blend of a curved surface and a flat base. This enigmatic shape, a staple of many mathematical problems, is symbolic of both simplicity and complexity. The surface area of a cone consists of the area covered by its base and the curved region wrapping around its axis. Now, working this out can seem daunting at first, but there’s a tool I frequently employ to demystify these calculations: Microsoft Excel. Excel’s grid-like structure and robust formula capabilities make it an ideal candidate to tackle the challenge.

 

Understanding the Cone in Mathematical Terms

The Significance of Pi in Cone Calculations

Pi (π) is key when calculating the surface area of cones. This famous number, about 3.14159, is important for anything involving circles—like the circular base of a cone. In cone formulas, π links the radius, height, and slant height, helping us find the lateral and total surface areas. Excel’s PI function gives π with high accuracy, up to 15 decimal places, making it perfect for precise calculations. This shows just how essential π is in geometry and in tools like Excel.

Key Cone Metrics: Radius, Height, and Slant Height

When dealing with the geometry of cones, three measurements are particularly essential—the radius, the height, and the slant height. The radius (r) of a cone’s base is half of its diameter, a line segment from one point on the circle through the center to another point on the circle. The height (h), on the other hand, is the perpendicular distance from the base to the apex of the cone. Lastly, the slant height (l) is the diagonal line that connects the apex to any point along the circular edge. Together, they are the primary dimensions needed to calculate the surface area.

For the curved surface area of a cone, we rely on π, r, and the slant height (l). Whereas, for the total surface area, we incorporate both the curved surface and the base area, including π, r, and h for the latter.

Calculate the Surface Area of a Cone in Excel

Syntax

The syntax for the Surface Area of a Cone in Excel is –

A = PI * r  (r*SQRT(+h^2+r^2))

• This function returns the value of Pi (π), which is approximately 3.14159.
• Pi is a mathematical constant used in calculations involving circles and curves (like the circular base of the cone).
• This represents the radius (r) of the cone, stored in cell A2.
• The radius is the distance from the center of the circular base to the edge of the base.
• SQRT() is the square root function. It finds the square root of a number.
• B2^2 is the square of the height (h) of the cone, stored in cell B2. This is the vertical distance from the apex (top point) to the center of the base.
• A2^2 is the square of the radius (r).
• SQRT(B2^2 + A2^2) calculates the slant height (l) of the cone. The slant height is the diagonal distance from the apex to the edge of the base. It forms the hypotenuse of a right triangle where the height and radius are the two other sides.
• This part adds the radius (r) and the slant height (l).
• The sum of these values represents the distance around the cone (the radius of the base plus the slant height).
• Finally, this whole part multiplies Pi (π), the radius (r), and the sum of the radius (r) and the slant height (l).
• This gives the total surface area of the cone, which is the area of the base plus the lateral surface area (the curved part).

What this formula calculates:

• The formula calculates the total surface area of the cone.
• The total surface area consists of two parts:
• The area of the circular base: This is calculated by πr2\pi r^2πr2, but the formula here combines it with the lateral surface area.
• The lateral surface area: This is the curved surface area, and it’s given by the formula πrl\pi r lπrl, where lll is the slant height.

Simplified Steps to Calculate

Calculating the surface area of a cone in Excel is a straightforward process. With just a few inputs—like the radius of the base and the slant height—you can easily find the surface area. This guide will take you through the simple steps to do it quickly in Excel.

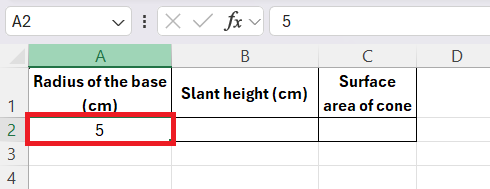
STEP 1: Type the radius of the cone’s base into a cell (for example, A2).

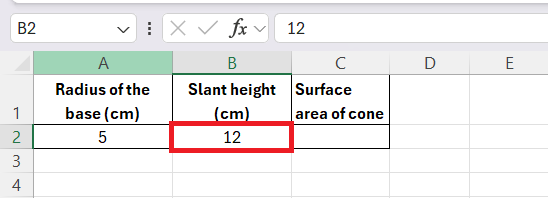
STEP 2: Enter the slant height of the cone into another cell (for example, B2).

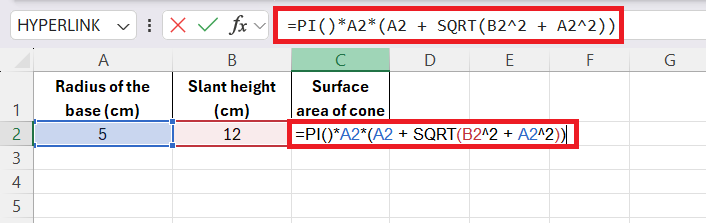
STEP 3: In a new cell, type this formula to calculate the surface area:

=PI()*A2*(A2 + SQRT(B2^2 + A2^2))

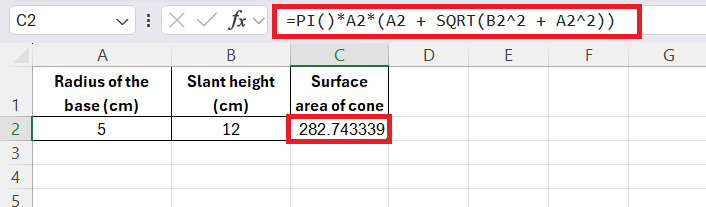
STEP 4: Hit Enter and Excel will instantly calculate the surface area of the cone.

 

FAQs on Surface Area of Cone

What is the surface area of a cone?

The formula for the total surface area of a cone is TSA = πr(r + l), where ‘r’ stands for the base radius and ‘l’ for the slant height. This includes both the base and the curved surface. If you only need the curved surface area, use CSA = πrl, where ‘l’ is still the slant height.

What Basic Geometric Knowledge Do I Need for Cone Calculations?

To effectively carry out cone calculations, you should understand the concepts of radius, height, slant height, and how they relate to a cone. Additionally, knowing the significance of π and being able to apply the Pythagorean theorem for determining slant height are crucial skills.

How Does Excel Simplify Complex Surface Area Problems?

Excel simplifies complex surface area problems by allowing for the automation of calculations through formulas that handle repetitive tasks and provide accurate results instantly. It consolidates multiple steps into one seamless process, reducing the chance of human error and saving time.

Can Excel Handle Both Total and Curved Surface Area of Cones?

Yes, Excel is well-equipped to handle both total and curved surface area calculations of cones. With the correct formulas in place, it can effortlessly manage these computations and provide quick, accurate results for various types of cones.

How to calculate the slant height of the cone?

To calculate the slant height of a cone, use the Pythagorean theorem formula: slant height (l) = √(r^2 + h^2), where ‘r’ is the radius and ‘h’ is the vertical height of the cone.