The Ultimate Guide to Excel PI – Surface Area of Cylinder Formulas

When I need to calculate the surface area of cylinder, Excel makes the process incredibly easy and efficient. By using the right formula and a few basic functions, I can handle this calculation without hassle. Let me walk you through how I set this up in Excel step by step.

Key Takeaways:

• Excel simplifies cylinder surface area calculations using precise functions like PI and POWER for efficient and accurate results.
• Organized data entry for radius and height ensuring clarity and smooth calculations in Excel.
• The PI function provides high-precision values of π, eliminating manual input errors in geometric formulas.
• Dynamic cell references in formulas allow automatic updates for recalculated surface areas.
• Troubleshooting tools like formula auditing and error-checking enhance accuracy and transparency in Excel workflows.

 

Unwrapping the Cylinder Surface Area Puzzle

The Geometry Behind Cylinders

Delving into the essence of hollow cylinders, I’m intrigued by their simplistic yet vital presence in our daily lives. Made entirely of two parallel circular bases linked by a curved side, these ordinary items – from straws to water pipes – surprisingly share the complexities found in three-dimensional geometry. Their surfaces wrap around an empty space, creating an intricate relationship between radius, height, and the mathematical constant π (pi).

Excel as Your Mathematical Companion

Discovering the full potential of Excel for geometric calculations is truly a game-changer. This powerful tool isn’t just for finance professionals; it also doubles as my mathematical brain, capable of handling complex calculations with ease. Excel’s sophisticated formula environment makes calculating the surface area of objects such as cylinders both accurate and efficient, thereby turning a potentially tedious task into a straightforward process.

With capabilities ranging from basic arithmetic to advanced functions, Excel stands as a steadfast ally in solving the cylinder surface area puzzle.

 

Master the PI Function in Excel

Defining the PI Function and Its Uses

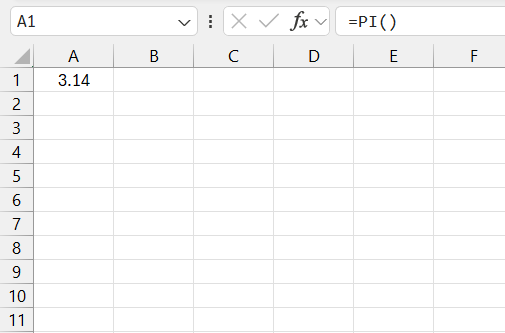
The PI function in Excel is a nifty feature that grants me access to the value of π with 15-digit precision, encapsulated in the simple syntax =PI().

This function is indispensable in calculations related to circles and cylindrical objects, playing a central role in determining areas and volumes where this fundamental mathematical constant is needed. By effortlessly providing an accurate value of π, the PI function averts the risk associated with manual input of π, which could potentially lead to errors.

Real-World Applications: Why PI Matters in Calculations

In practice, π extends far beyond the realm of academic exercises and enters the domain where precision dictates the success of our constructions and products. Take, for example, the manufacture of automotive parts where wheels and axles must adhere to exact dimensions for safe and efficient performance. Or consider the field of architecture, where circular design elements necessitate precise calculations, ensuring structural integrity.

Whether it’s measuring irrigation systems for farmland or designing a coffee cup, π makes the calculation of curved surfaces possible, reflecting how a simple Greek letter can have implications on outcomes that are both practical and profound.

 

Step-by-Step Guide to Calculating Surface Area of Cylinder

Entering the Data for Your Cylinder

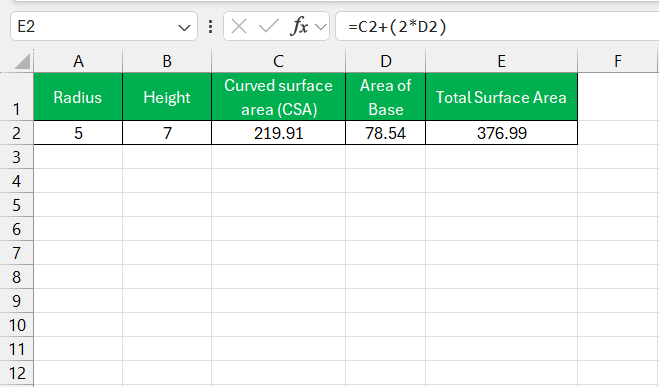
When it’s time to calculate a cylinder’s surface area in Excel, the initial step involves accurately entering the data for radius and height. As a routine, I create a well-organized worksheet with labeled columns for these parameters – one for the radius (r) and another for the height (h) of the cylinder.

It’s crucial to determine and use consistent units to ensure the results are in the desired unit of area. By arranging this data neatly, I not only pave the way for a smooth calculation process but also enhance the clarity and traceability of the information.

Formula Crafting: Total, Base, and Curved Surface Areas

Crafting formulas in Excel requires a well-thought-out approach that aligns with geometric principles. For the uninitiated, the total surface area (TSA) of a cylinder is the sum of the curved surface area (also called the lateral surface area) and the area of the two circular bases. To break it down:

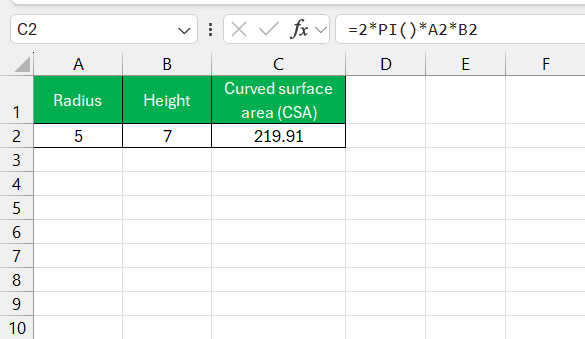
• For the curved surface area (CSA), I use the formula =2*PI()*radius*height.

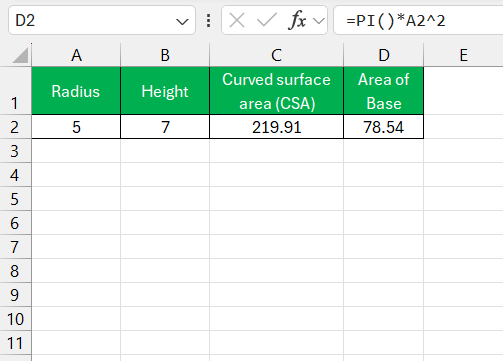
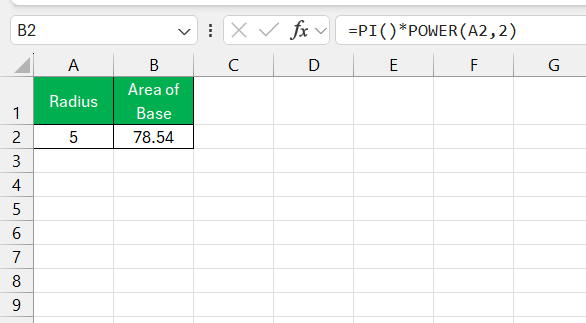
• To calculate the area of one base, the formula is =PI()*radius^2. Since there are two bases, I multiply this result by two for the TSA.

• The formula for the TSA then becomes = Curved Surface Area + 2 * Area of Base

I carefully input these formulas in Excel, using cell references for radius and height to ensure dynamic calculations that update automatically with any changes in the input data.

 

Tips & Tricks

Troubleshooting Common Errors and Tips for Accurate Results

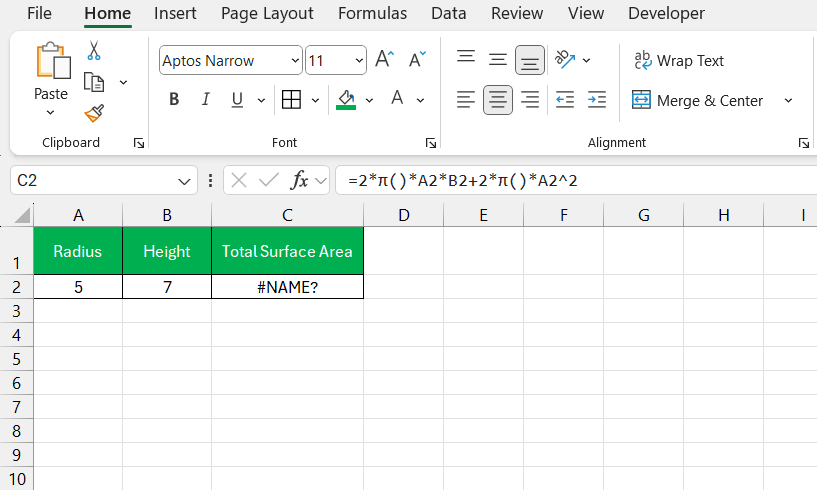
Navigating errors in Excel is a substantial aspect of my routine, one that reinforces the importance of scrupulousness in formula entry. A recurring challenge is an incorrect syntax leading to #NAME? error.

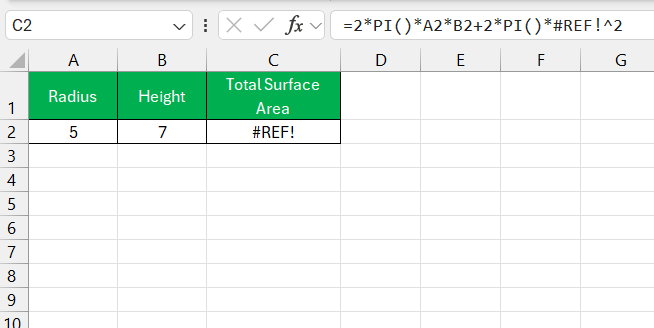
When a cell reference is mistyped leading to #REF! error.

To mitigate such issues, double-checking formulas before hitting enter is a habit I cultivate. Moreover, using Excel’s built-in formula auditing tools aids in tracing precedents and dependents, unraveling the web of connections between cells.

For heightened precision, I take advantage of Excel’s “Increase Decimal” feature to reveal more decimal places.

 

Functions that Partner with PI for Enhanced Calculations

POWER Function: Exponentiation Made Easy

The POWER function is like a trusted comrade that simplifies raising numbers to their respective powers. By adopting the syntax =POWER(number, power), where “number” is the base and “power” is the exponent, I find it especially useful when squaring or cubing numbers, which is commonplace in geometry.

For instance, squaring the radius of a circle in cell A2 is as simple as =POWER(A2, 2) function excels when I wish to avoid potential errors that might arise from manual squaring or when the formula needs to be more transparent to those who may not be familiar with Excel’s caret (^) operator.

FAQs on Surface Area of Cylinder

What is the Formula to Find the Base Area of a Cylinder?

The base area of a cylinder is the area of its circular base, which I can calculate using the formula π * r^2. In Excel, I can apply this formula as =PI() * radius^2, where radius is the radius of the cylinder’s base. This formula gives me the area of one base, and since the cylinder has two identical bases, I would multiply the result by 2 if I needed the total area of both bases.

How to Calculate Surface Area of Cylinder Using Calculator?

To calculate the surface area of a cylinder, I need to sum the lateral surface area and the area of the two circular bases. The lateral surface area is calculated as 2 * π * r * h, and the area of the bases is 2 * π * r^2. I can add these two values together to get the total surface area. In Excel, the formula would be =2 * PI() * radius * height + 2 * PI() * radius^2.

What is the formula for the surface area of a circle in Excel?

The surface area of a circle is simply its area, which I calculate using the formula π * r^2. In Excel, I can write this as =PI() * radius^2, where radius is the radius of the circle. This formula provides the total area inside the circle.

What is surface area?

Surface area refers to the total area of the exterior surface of a 3D object. It includes all the outer surfaces, such as the sides, tops, and bottoms. For example, in the case of a cylinder, it includes the lateral surface (the curved part) and the two circular bases.

What is the circumference?

The circumference of a circle is the distance around its boundary, and it can be calculated using the formula 2 * π * r. In Excel, I can calculate this as =2 * PI() * radius, where radius is the radius of the circle. The result gives me the perimeter or the boundary length of the circle.