When working with Excel, I often find myself needing to calculate different geometrical values, including the volume of a cone. Instead of manually using the mathematical formula each time, I can leverage Excel’s powerful functions to automate this calculation efficiently. In this guide, I’ll walk you through the step-by-step process of calculating the volume of a cone in Excel.
Key Takeaways:
- Excel simplifies cone volume calculations using the formula =(1/3)*PI()radius^2height.
- Using named ranges improves formula readability and prevents confusion.
- Maintaining consistent units prevents calculation errors and incorrect results.
- Common Excel errors like #VALUE! and #DIV/0! can be resolved by checking formulas and input data.
- Advanced applications include truncated cones, spheres, and industry-specific volume calculations.
Unraveling the Cone’s Volume Mystery in Excel
Introduction to Volume of a Cone
Understanding the volume of a cone is crucial for numerous applications ranging from academic to real-world scenarios. A cone’s volume represents the space it occupies and is calculated using the formula V = 1/3 * π * r^2 * h, where r is the radius of the base circle, and h is the height of the cone. This formula applies to right cones, where the apex is directly above the center of the base, and oblique cones alike.
The Role of PI in Volume Calculation
Pi (π) is a fundamental constant in geometry, vital for calculating the volume of curved shapes like cones. Its omnipresence in circular measurements makes it a cornerstone for precise volumetric calculations. In a volume formula, π links the radius of a cone’s base to its height, playing an essential role in finding the internal capacity of the cone.
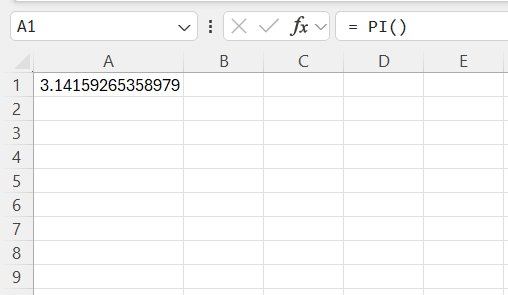
Using π, represented in Excel with the =PI() function that gives us an accurate value up to 15 decimal places, we can ensure that our volumetric computations resonate with mathematical precision.
Setting the Stage for Calculation
Step 1: Define the Necessary Parameters
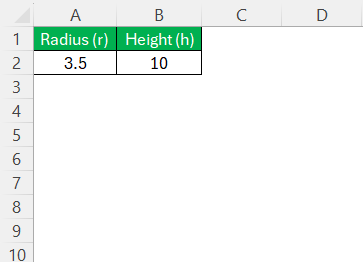
Before I can harness Excel’s computational power to determine a cone’s volume, I must identify and input the necessary parameters. For a cone, two critical measurements are required: the radius of the base (r) and the height (h) of the cone. In Excel, I’ll arrange these parameters in individual columns, clearly labeled to avoid confusion.
For example, I might place the radius in column A and the height in column B.
Remembering to save the workbook after inputting these measurements ensures that none of this essential groundwork is lost.
Step 2: Laying Down the Formula Structure
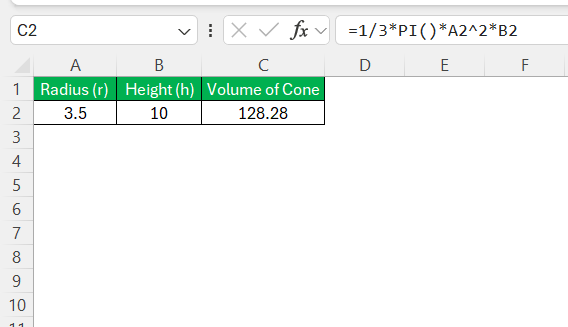
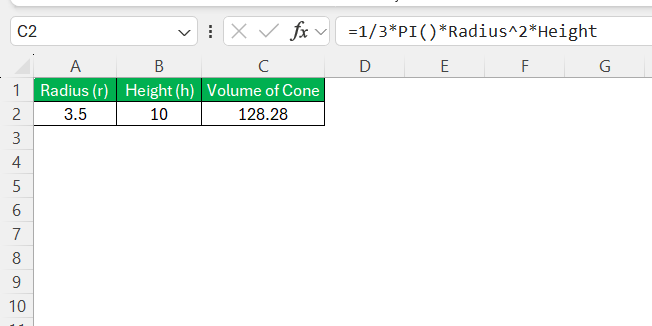
Once I have defined the radius and height in my Excel sheet, it’s time to lay out the proper structure for the volume calculation formula. Considering the volume of a cone is calculated by the formula ( 1/3 * pi * r^2 * h ), in Excel, the corresponding cell where I want the result should contain the formula structured as ( =1/3 * PI() * A2^2 * B2 ) if A2 holds the radius value and B2 the height.
This ensures that when the data is entered correctly, Excel can seamlessly perform the calculations.
Using Named Ranges for Better Readability
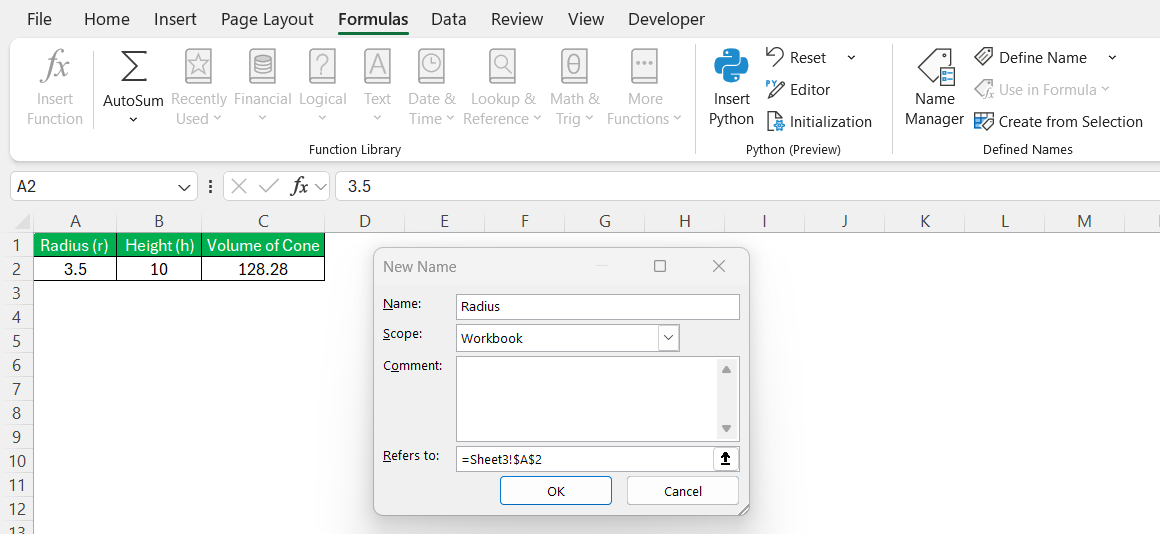
To make the formula more intuitive, I can assign names to the cells:
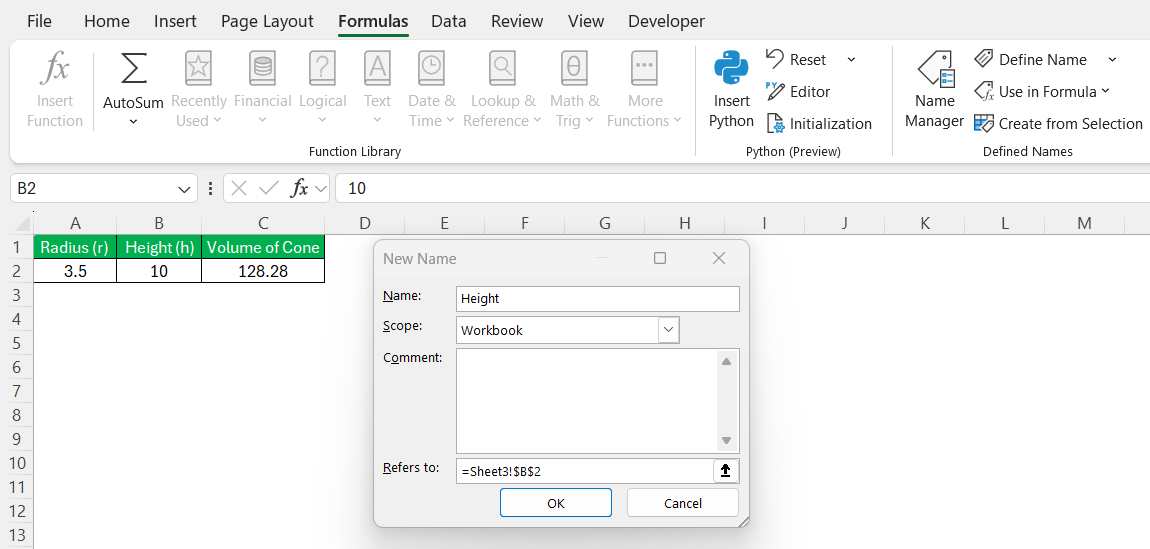
STEP 1: Select A2, go to the Formulas tab, and click Define Name. I name it Radius.
STEP 2: Select B2, go to the Formulas tab, and click Define Name. I name it Height.
STEP 3: Now, I update my formula using the named ranges:
= (1/3) * PI() * Radius^2 * Height
This makes the formula easier to read and understand.
Tips for Excel Formula Success
Ensuring Accuracy with Unit Consistency
Ensuring accuracy in Excel formulas, particularly when calculating volume, hinges on maintaining unit consistency. All measurements, whether in meters, centimeters, inches, etc., must be in the same unit system throughout your worksheet. Mixing units can lead to glaringly incorrect calculations. Therefore, before starting with any computations, I verify that my measurements adhere to the same unit system to avert such headaches.
Troubleshooting Common Excel Errors
When troubleshooting common Excel errors in volume calculations, several proactive steps can save time and frustration. For instance, if I see “#VALUE!” or “#DIV/0!”, I immediately check my formulas for mistakes and confirm that all required cells contain the correct data while ensuring I’m not inadvertently dividing by zero. If results seem off, I double-check my formulas, data, and units because even a small miscalculation can lead to significant discrepancies. Diligence in these checks often reveals and rectifies the issue.
Advancing Your Excel Skills
Leveraging the Formula for Different Scenarios
Once I grasp the cone volume formula, leveraging it for different scenarios becomes an exercise in creativity and efficiency. I might apply this formula to calculate the volume of an ice cream cone inventory, to determine wax volume for candle making, or even to estimate soil needed for a conical garden bed. By adjusting the formula to fit the scenario’s specifics, I extract immense value from Excel’s calculating prowess, tailoring it to diverse needs and industries.
Exploring Advanced Volume Calculations
Exploring advanced volume calculations in Excel often involves delving into more complex geometrical shapes and combining different formulae. For shapes like truncated cones, spheres, or irregular polyhedra, I can expand my use of Excel’s mathematical functions.
For instance, calculating the volume of a truncated cone would require the application of both the PI function and additional calculations for the different radii and heights. Embracing such complex scenarios broadens my mastery of Excel’s capabilities for volumetric analysis.
FAQ: Excel and Volume of a Cone
What is the formula for the volume of a cone in Excel?
In Excel, the formula to calculate the volume of a cone is =(1/3)*PI()*radius^2*height. Replace ‘radius’ and ‘height’ with the corresponding cell references that contain those values.
How do you convert units in Excel when calculating volume?
To convert units in Excel when calculating volume, multiply the original measurement by a conversion factor to change it to the desired unit. For clarity, use separate cells to define the conversion rate.
What are some common mistakes when using the PI function?
Common mistakes when using the PI function include not using parentheses correctly, multiplying with an incorrect radius or height, forgetting to use the function altogether, and entering an inaccurate value for π manually.
What is the volume of frustum?
The volume of a frustum is calculated using the formula (V =1/3 * H * (S1 + S2 + SQRT(S1*S2))), where (H) is the height, (S1) and (S2) are the areas of the two bases.
What is the surface area of a cone?
The surface area of a cone is found with (TSA = PI * r(r + l)), where (r) is the radius of the base and (l) is the slant height, including both the base and the lateral surface area.
John Michaloudis is a former accountant and finance analyst at General Electric, a Microsoft MVP since 2020, an Amazon #1 bestselling author of 4 Microsoft Excel books and teacher of Microsoft Excel & Office over at his flagship MyExcelOnline Academy Online Course.